Question

If the area of a right triangle is 15, what is its perimeter?

Answer 1

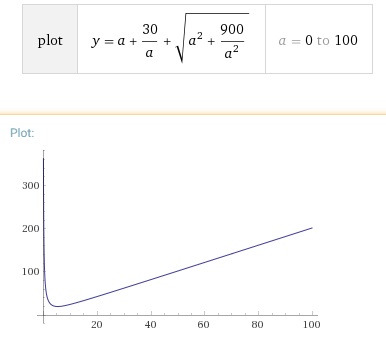
The perimeter is given as a function of side `a` via `p = a + 30/a + sqrt{a^2 + 30^2/a^2}` which has a minimum at `a=sqrt{30}` and is unbounded, no maximum.

Explanation:

It could be almost anything. Call the sides `a` and `b` and the hypotenuse `c`. Of course

`c^2 =a^2 + b^2`

We know

`1 /2 a b = 15`

`b = 30/a`

`c^2 = a^2 + (30/a)^2 = a^2 + 900/a^2`

`c = sqrt{ a^2 + 900/a^2 }`

Call the periimeter `p`:

`p = a+b+c = a + 30/a + sqrt{a^2 + 900/a^2}`

That's a function with a minimum at `a=sqrt{ 30}` (for positive `a`) and is unbounded, no maximum.