If #x+2# is a factor of #f(x)=2x^3-3x^2-4x+a# , find the value of #a#?

Question

5771 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-28T18:19:59

#a=20#

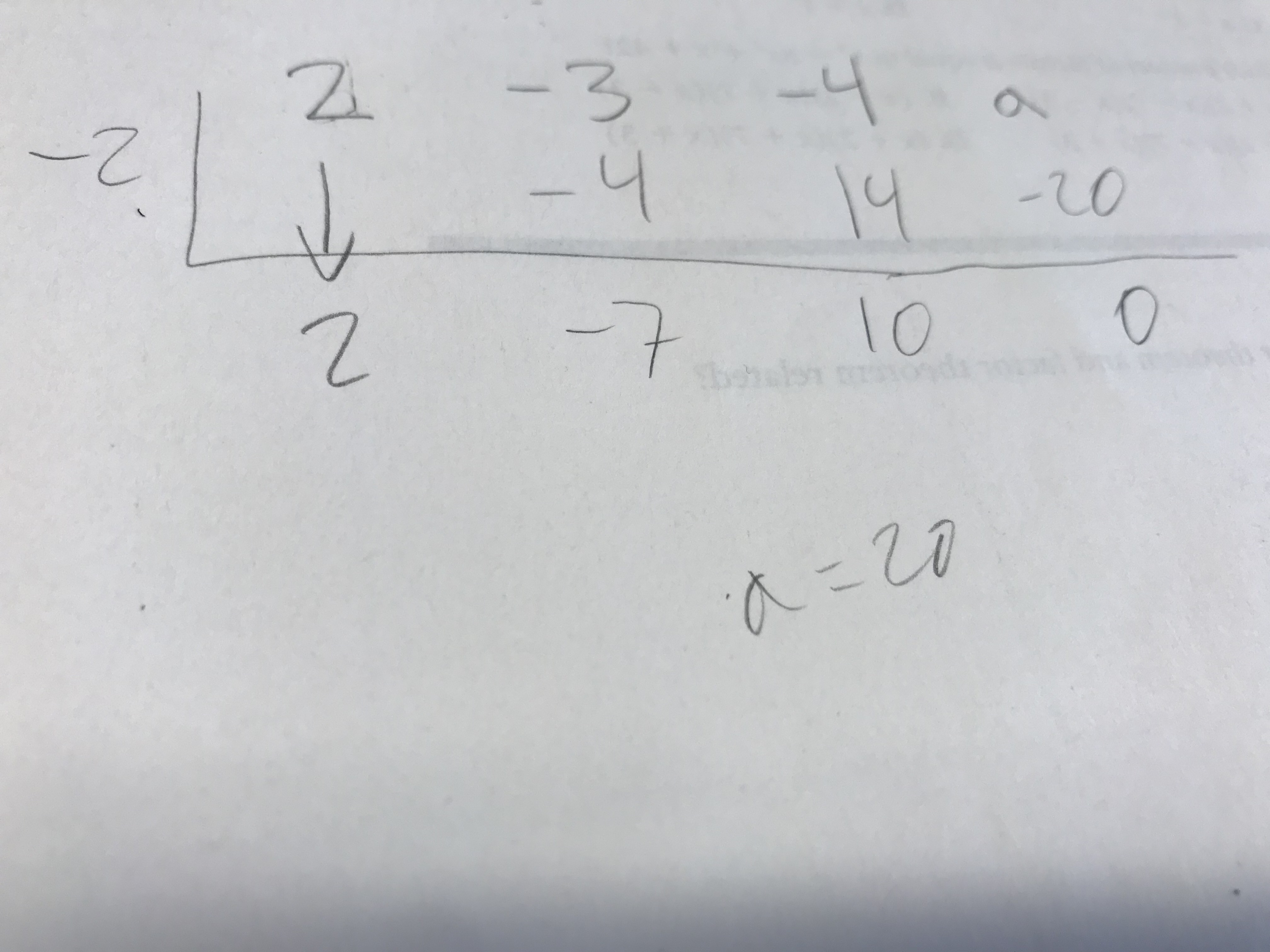
enter image source here

Write down the coefficient numbers in the first row in order of highest to lowest power and the factor.

#x+2 (x-m) m=-2#

Drag the first coefficient number down, #2xx(-2)=-4#, write #-4# under the next coefficient number, #-3+(-4)=-7#, #(-2)xx(-7)=14#, repeat...

We want the denominator to be zero, so

#a+(-20)=0#

#a=20#

Answer 2 · 2018-02-28T18:41:06

#a=20#

#"given "x+2" is a factor then "x=-2" is a zero"#

#rArrf(-2)=2(-2)^3-3(-2)^2-4(-2)+a=0#

#rArr-16-12+8+a=0#

#rArra=20#