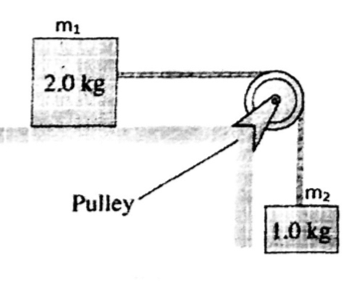
In a pulley system, #m_1# is #2.0kg# and #m_2# is #1.0kg#. The coefficient of kinetic friction between #m_1# and the table is #mu_k=0.15#. What is the acceleration of the pulley system?
1 Answer
Jun 17, 2016
Explanation:
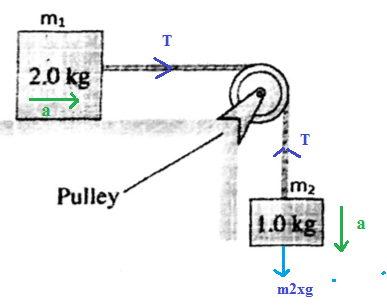
GIVEN
#m_1=2 kg , m_2 =1kg# -
#"Coefficient of kinetic friction between " m_1 " and table" (mu_k)=0.15# -
# "Let"#
#color (blue) T " be tension on string"#
#" and " color(green) a" be the acceleration of the system "#
Now considering the forces on
Normal reaction
Resisting force of kinetic friction
Gravitational pull on
So for
Considering the forces on
Adding equation (1) and equation(2) we get

