In a quadrilateral ABCD, P and R are the midpoints of AB and CD respectively. Also, Q and S are points on the sides BC and DA respectively such that BQ=2QC and DS=2SA. Prove that the area of the quadrilateral PQRS equals to half of the area of ABCD?
1 Answer
Indeed
Explanation:
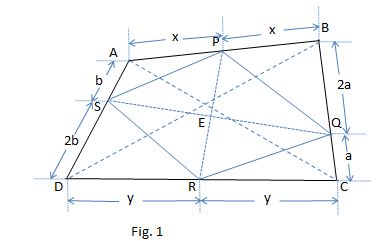 I created this figure using MS Excel
I created this figure using MS Excel
There's a simple way to solve this problem using Vectorial Product (in case cross product).
The formula for a quadrilateral's area using vectors is discussed in
Quadrilateral's area using vectors
So the area of a quadrilateral is given by
(Let's remind that
In case:
To be able to compare the results we should get the vectors as function of other vectors in common. In this problem, it will be convenient to get the vectors of the diagonals as function of
Quadrilateral ABCD
So
Quadrilateral PQRS
PvecD=PvecS+SvecD -> note thatSvecD=2AvecS
PvecD=PvecS+2AvecS -> note thatAvecS=AvecP+PvecS
PvecD=PvecS+2(AvecP+PvecS) =>3PvecS=(PvecD-2AvecP) =>PvecS=(PvecD-2AvecP)/3 -> note thatPvecD=PvecR+RvecD=PvecR-DvecR
-> PvecS=(PvecR-DvecR-2AvecP)/3
PvecC=PvecQ+QvecC -> note thatQvecC=(BvecQ)/2
PvecC=PvecQ+(BvecQ)/2 -> note thatBvecQ=BvecP+PvecQ (sinceBvecP=-AvecP =>BvecQ=-AvecP+PvecQ)
2PvecC=2PvecQ-AvecP+PvecQ =>3PvecQ=2PvecC+AvecP =>PvecQ=(2PvecC+AvecP)/3 -> note thatPvecC=PvecR+RvecC=PvecR+DvecR
PvecQ=(2PvecR+2DvecR+AvecP)/3 Back to
SvecQ
SvecQ=SvecP+PvecQ=-PvecS+PvecQ
SvecQ=(-PvecR+DvecR+2AvecP)/3+(2PvecR+2DvecR+AvecP)/3
SvecQ=(PvecR)/3+DvecR+AvecP
S_(PQRS)=(1/2)*|PvecR xx SvecQ|=(1/2)|PvecR xx ((PvecR)/3+DvecR+AvecP)|
S_(PQRS)=(1/2)*|PvecR xx (DvecR+AvecP)|
Finally,
Q.E.D.

