Initially switch is open, no charge on the capacitor, (a) Close the switch, find #I_i, (i = 1, 2, 3) Q, & V_C# immediately after. (b) Switch is closed for long find #I_i, Q & V_C#. (c) Find #I_i, Q, & V_c# immediately reopened? d) Reopened for long?
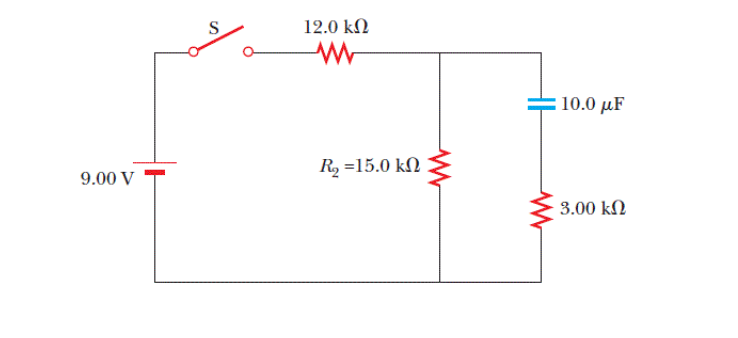
Calling #R_1=12.0Omega#, #R_3=3.00Omega#, #E = 9.00V# and #C = 10.0muF#
After closing the switch we have
#{(E = I_1 R_1+(I_1-I_2)R_2),
(1/C int_0^tI_2dt +I_2 R_3+(I_2-I_1)R_2=0)
:}#
but #Q = int_0^t I dt# so the equations can be stated as
#{
(E = dotQ_1 R_1+(dotQ_1-dotQ_2)R_2),
(1/C Q_2 +dotQ_2 R_3+(dotQ_2-dotQ_1)R_2=0)
:}#
Solving for #dotQ_1# and #dotQ_2# we get
#{
(dotQ_1 =(C E- Q_2)/(C (R_1 + R_3))),
(dotQ_2 = (C E (R_2-R_3) - Q_2 (R_1+R_2))/(C (R_1 R_2 + R_2 R_3))):}#
Calling
#alpha_1=(R_2-R_3)/ (R_1 R_2 + R_2 R_3)# and
#alpha_2 = (R_1+R_2)/(C (R_1 R_2 + R_2 R_3))#
#beta_1=1/(R_1+R_3)# and
#beta_2=1/(C(R_1+R_3))# we have
#{
(dotQ_1+beta_2Q_2=beta_1E),
(dotQ_2+alpha_2Q_2=alpha_1E):}#
Solving the differential equations we have
#{
(Q_2(t)=c_2e^(-beta_2 t)+(beta_1)/(beta_2)E),
(Q_1(t)=c_2e^(-beta_2 t)+c_1):}#
where #c_1# and #c_2# are integration constants to be defined according to the initial conditions.
Answering the required items
(a) At the very init #Q_2(0)=0# so we have
#c_2+(beta_1)/(beta_2)E=0# so #c_2=-(beta_1)/(beta_2)E#
also
#Q_1(0)=0# so we have
#c_2+c_1=0# then #c_1=(beta_1)/(beta_2)E# and the charge equations are
#Q_1=-(beta_1)/(beta_2)E(1-e^(-beta_2t))# and
#Q_2=(beta_1)/(beta_2)E(1-e^(-beta_2t))#
Analogously
#I_1= dot Q_1=-beta_1Ee^(-beta_2t)# and
#I_2=dot Q_2=beta_1Ee^(-beta_2t)#

