Question

Iodine-131 is a radioactive isotope with a half-life of 8 days. How many grams of a 64 g sample of iodine-131 will remain at the end of 24 days?

Answer 1

`"8 g"`

Explanation:

The nuclear half-life of a radioactive isotope tells you how much time must pass in order for half of the atoms present in an initial sample to undergo radioactive decay.

In essence, the half-life tells you at what time intervals you can expect an initial sample of a radioactive isotope to be halved.

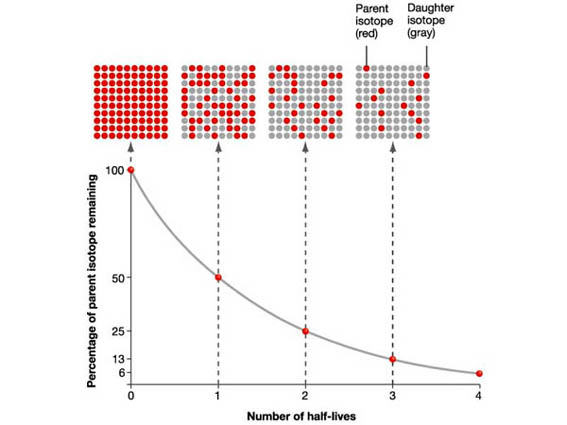
In your case, iodine-131 is said to have a half-life of `8` days. This means that with every `8` days that pass, your sample of iodine-131 will be halved.

If you take `A_0` to be the initial sample of iodine-131, you will be left with

`1/2 * A_0 = A_0/2 ->` after the passing of one half-life

`1/2 * A_0/2 = A_0/4 ->` after the passing of two half-lives

`1/2 * A_0/4 = A_0/8 ->` after the passing of three half-lives
`vdots`

and so on.

You can thus say that the amount of iodine-131 that remains undecayed, `"A"`, after a period of time `t`, will be equal to

`color(blue)(|bar(ul(color(white)(a/a)A = A_0 * 1/2^ncolor(white)(a/a)|)))`

Here `n` represents the number of half-lives that pass in `t`.

In your case, you have

`n = (24 color(red)(cancel(color(black)("days"))))/(8color(red)(cancel(color(black)("days")))) = 3`

This will get you

`A_"24 days" = "64 g" * 1/2^3`

`A_"24 days" = color(green)(|bar(ul(color(white)(a/a)"8 g"color(white)(a/a)|)))`

Answer 2

`=> m_t = 8g`

Explanation:

Half Life follows first Order kinetics

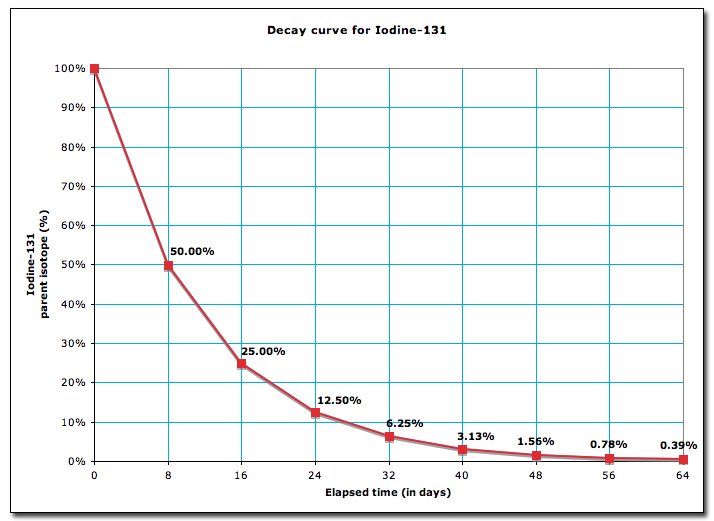
This graph shows what is going on during the decay

As you can see from the graph the half life is 8 days

Lets do the math and verify it with the graph

Recall

`t_(1/2) = ln2/k`

`8 = ln2/k`

`k = ln2/8`

With this you can solve most problems regarding the above data

`ln(A_o/A_t) = kt`

`ln(A_o/A_t) = ln2/8 * 24 = 3 ln2 = ln 2^3 = ln8`

`(A_o/A_t) = 8`

Now

Greater the concentration of a sample greater the mass in in it

`C prop M`

So

`(A_o/A_t) = (m_o/m_t) = 8`

`"we have "m_o = 64 g"`

`64/m_t = 8`

`=> m_t = 8g`

Verifying with the graph

`m_("24 hours") = 12.5 % m_o = 12.5 *10^-2 *m_o`
`=12.5 *10^-2 *64 = 8g`

Hence verified