Question

Is there an easy way to remember the order of filling of orbitals without diagram?

Answer 1

Well, you'll always be given a periodic table, whether during a test or simply by looking it up, so you can use the periodic table to remember most of it. Just sit down and get to know the periodic table. Break down the patterns into chunks and remember each chunk.

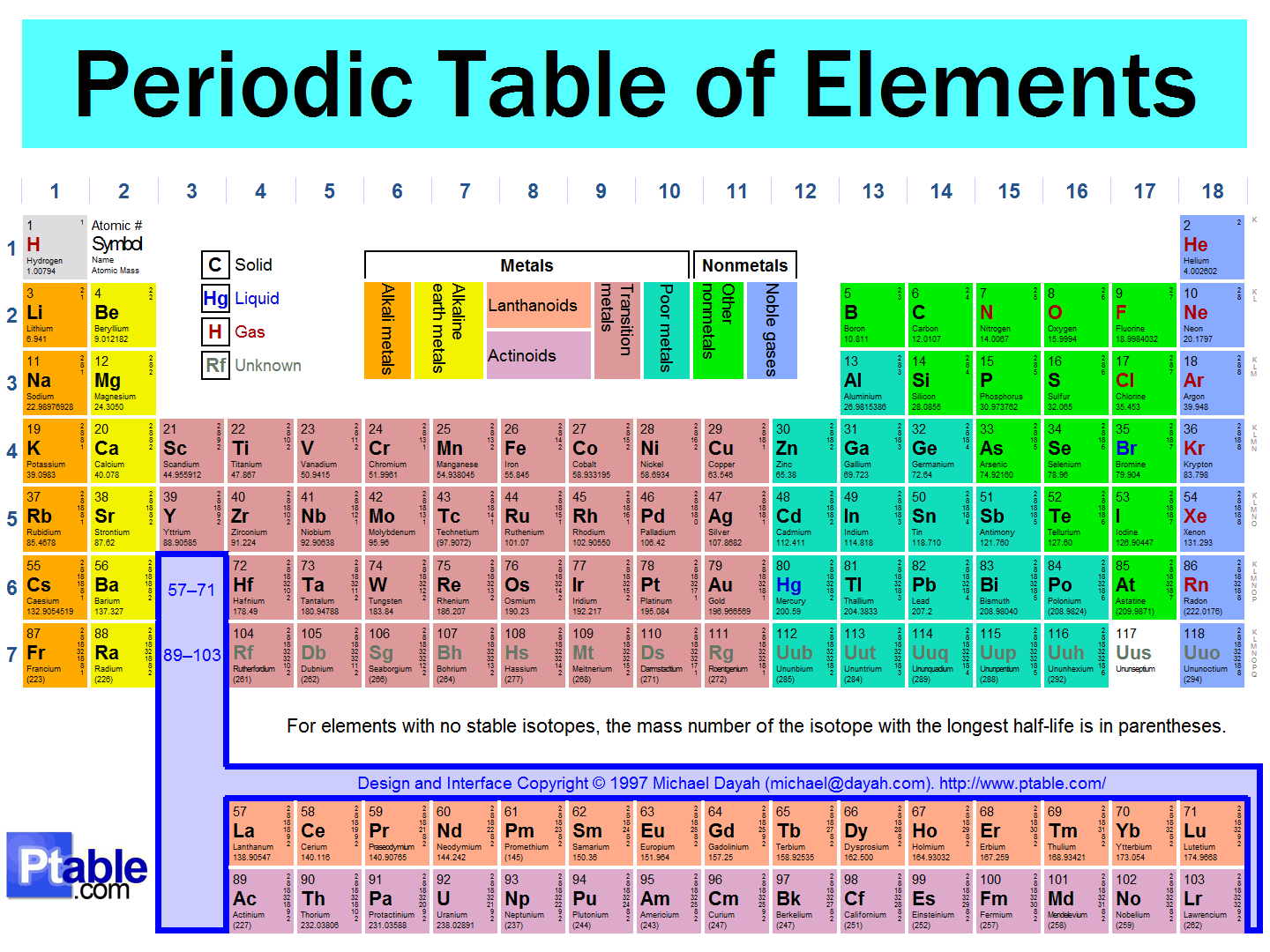
In general, for the first three rows:

• The principal quantum number `n` corresponds to the row number.
• The particular block corresponds to a new angular momentum quantum number `l`, except for the first row.

For these three rows, the "`s`" block is the first two columns, and the "`p`" block is the last six columns.

So, we start with `1s^2`, then move to row `2`, which gives `2s^2 2p^6`. The third row gives `3s^2 3p^6`.

For the fourth and fifth rows, since we already passed `n = 3`, we can start talking about the `3d` orbitals, so:

• We jump down to the `3d` "temporarily" after the first two `4s` electrons, and jump "back up" to the six `4p` electrons.
• We jump down to the `4d` "temporarily" after the first two `5s` electrons, and jump "back up" to the six `5p` electrons.
• We still have that the particular block corresponds to a different angular momentum quantum number `l`. We just now have that the "`d`" block is the middle `bb(10)` columns, for these two rows.

So, we supposedly continue as `4s^2 3d^10 4p^6` and `5s^2 4d^10 5p^6` for the fourth and fifth rows.

We should note however that these are only expected filling orders, and not what we indefinitely see for every single heavy element!

At the sixth and seventh rows, the elements start using the `f` orbitals.

• We jump down to the `4f` "temporarily" after the first two `6s` electrons, and jump "back up" to the ten `5d` electrons and next six `6p` electrons.
• We jump down to the `5f` "temporarily" after the first two `7s` electrons, and jump "back up" to the ten `6d` electrons and next six `7p` electrons.
• We still have that the particular block corresponds to a different angular momentum quantum number `l`. We just now have that the "`f`" block is the separate `bb(14)` columns, for these two rows.

So, we supposedly continue as `6s^2 4f^14 5d^10 6p^6` and `7s^2 5f^14 6d^10 7p^6`.

Again, we should note however that these are only expected filling orders, and not what we indefinitely see for every single heavy element!

So, just sit down and get to know the periodic table. Break down the patterns into chunks and remember each chunk.

If you know how to read it, you can determine expected filling orders as muscle memory, and remember exceptions like `"Cr"`, `"Mo"`, `"Cu"`, `"Ag"`, and `"Au"`.