It takes about #10^16# years for just half the samarium-149 in nature to decay by alpha-particle emission. What is the decay equation, and what is the isotope that is produced by the reaction?
1 Answer
The alpha decay of samarium-149 produces neodymium-145.
Explanation:
When a radioactive isotope undergoes alpha decay, its nucleus emits an
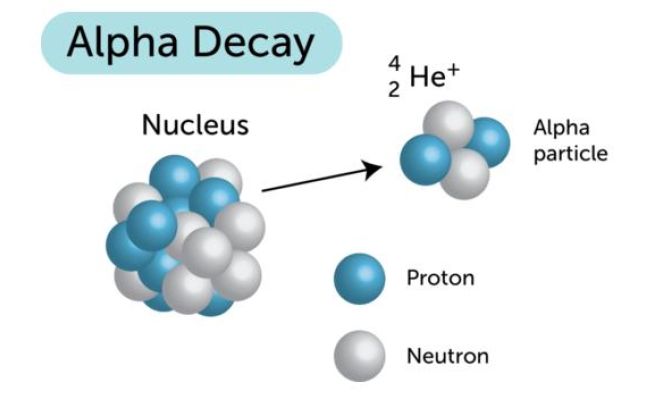
Pull up a periodic table and look for the atomic number of samarium,
#""_62^149"Sm" -> ""_x^ycolor(blue)(?) + ""_2^4"He"#
Your goal now is to find the values of
At this point, it's important that you're familiar with isotope notation.

For samarium-149, you have an atomic number equal to
#149 = y + 4 -># conservation of mass number
#62 = x + 2 -># conservation of charge
You will thus get
#{(y = 149 - 4 = 145), (x = 62 -2 = 60) :}#
The element that has an atomic number equal to
The alpha decay of samarium-149 will thus produce neodymium-145 and an alpha particle.
#""_62^149"Sm" -> ""_60^145"Nd" + ""_2^4"He"#

