Joel and Wyatt toss a baseball. The height in feet, of the baseball, above the ground is given by h(t) = -16t^2+55t+6, where t represents the time in seconds after the ball is thrown. How long is the ball in the air?
2 Answers
I found
Explanation:
This is intriguing...!
I would set
in fact if you set
So
Solving using the Quadratic Formula:
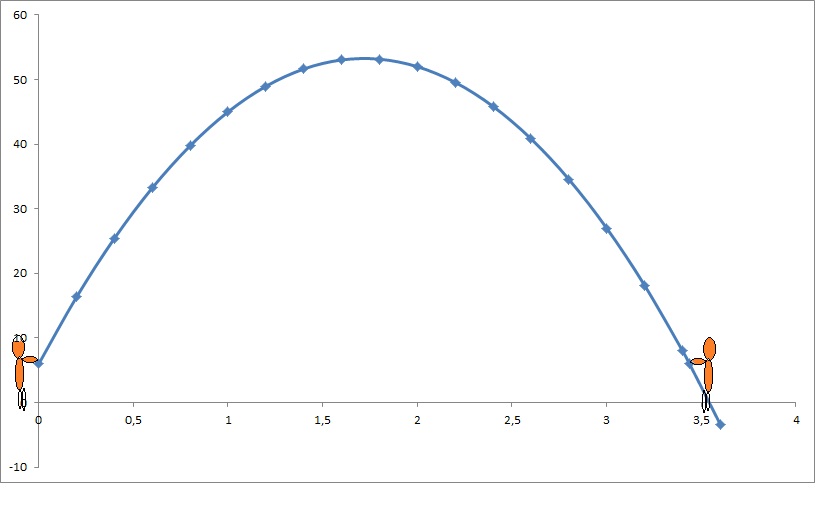
We have two variables...
Explanation:
There are two variables in this problem, the height of the ball
But we do know one of these. Perhaps looking at a picture will help:
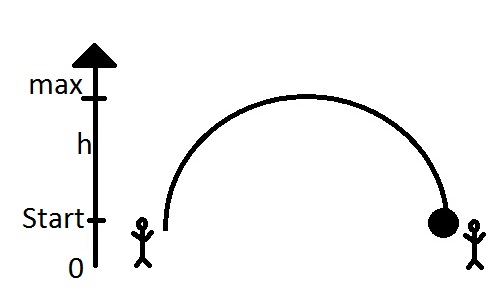
The ball travels at an arc when it's thrown, and we're never told the height at any point... but we can figure out the height at exactly two times: The moment before the ball is thrown, and the moment the ball is caught at the other end. One of those times is t = 0 (the ball hasn't been thrown yet).
So, if
So, now we know that the ball is starting at height = 6 feet. We also know that, once it's thrown, it has to come back down again, and at the end of its flight, it should be right where it started... 6 feet. So, there are two times at which the ball is at 6 feet. Right before it's thrown, and right when it's caught. That last time is what we're being asked to figure out here.
So,
Holy smokes, that's exactly the form we need to use the quadratic formula!

In this case,
We plug those numbers into the quadratic formula to find:
OR
Just to be sure, if we plug that number back into the equation, what height is the ball at when
6 feet, right where it started


