Let R be the region in the first quadrant bounded by the x-axis, the graph of #x=y^2+2#, and the line x=4. What is a the interval for the area of R?

Question

11077 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-08-28T23:39:40

#x# goes from #2# to #4# and #y# goes from #0# to #sqrt2#.

Sketch the graph of #x = y^2+2# by sketching the sideways parabola #x = y^2# then adding #2# to the #x# coordinates (translate #2# to the right).

Add the #x# axis and the vertical line #x = 4# to the picture:

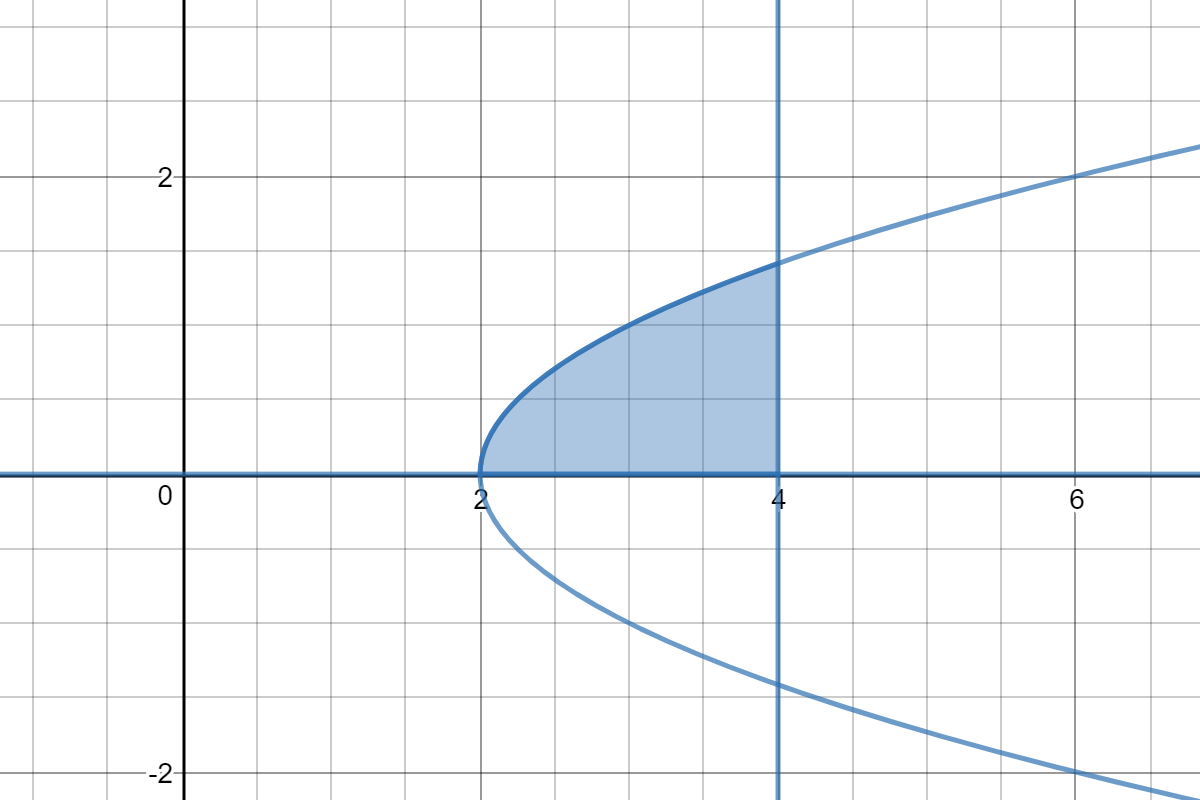
enter image source here

The area can be found by either

#int_2^4 sqrt(x-2)color(white)"/"dx#

or by

#int_0^sqrt2 (4-(y^2+2)) color(white)"/"dx#