Question

Let R be the region in the first quadrant that is enclosed by the graph of `y=tan x`, the x-axis, and the line x=pi/3, how do you find the area?

Answer 1

ln2

Explanation:

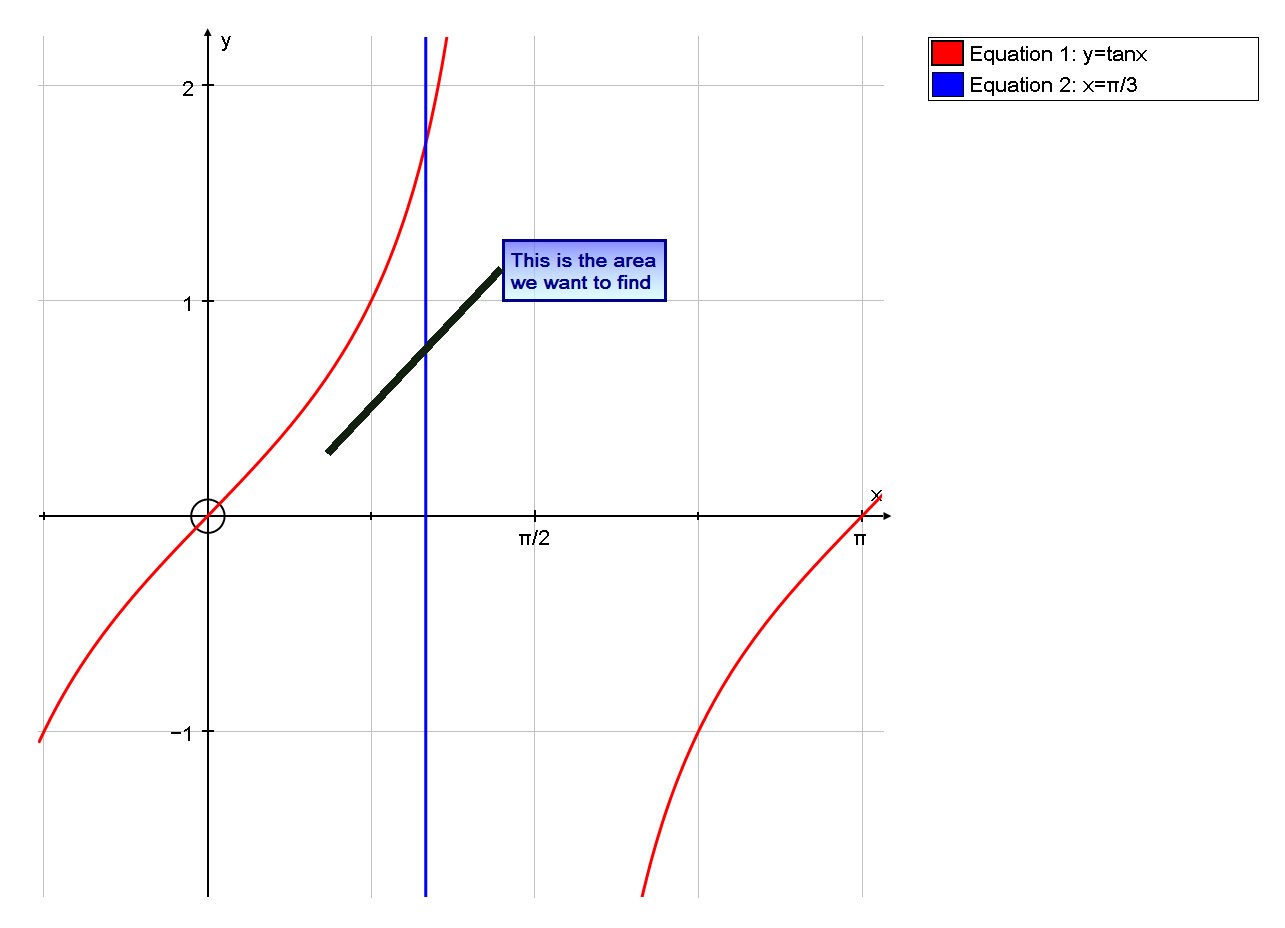
The area is given by integration with appropriate bounds

`:. A = int_0^(pi/3) tanx dx`
`:. A = int_0^(pi/3) sinx/cosx dx` .... [1]

Which we can integrate using a substitution

# { ("Let "u=cosx,=>,(du)/dx=-sinx), ("When "x=0,=>,u=cos0=1), ("And "x=pi/3,=>,u=cos(pi/3)=1/2) :} #

`:. int ... du = int ... -sinxdx`

Substituting into [1] we get

`A = int_1^(1/2) (-1/u)du`
`:. A = int_(1/2)^1 1/udu` (using `int_a^b...=-int_b^a...`)
`:. A = [lnu]_(1/2)^1`
`:. A = ln(1)-ln(1/2)`

`:. A = 0-ln(1/2)_` (as `ln(1) =0`)
`:. A = ln(2)`