Question

Let `vec(x)` be a vector, such that `vec(x) = (−1, 1), " and let " R(θ) = [(costheta, -sintheta), (sintheta, costheta )]`, that is Rotation Operator. For `theta=3/4pi` find `vec(y) = R(theta)vec(x)`? Make a sketch showing x, y, and θ?

Answer 1

This turns out to be a counterclockwise rotation. Can you guess by how many degrees?

---

Let `T:RR^2 |-> RR^2` be a linear transformation, where

`T(vecx) = R(theta)vecx,`
`R(theta) = [(costheta,-sintheta),(sintheta,costheta)],`
`vecx = << -1,1 >>.`

Note that this transformation was represented as the transformation matrix `R(theta)`.

What it means is since `R` is the rotation matrix which represents the rotational transformation, we can multiply `R` by `vecx` to accomplish this transformation.

`[(costheta,-sintheta),(sintheta,costheta)]xx<< -1,1 >>`

For an `MxxK` and `KxxN` matrix, the result is an `color(green)(MxxN)` matrix, where `M` is the row dimension and `N` is the column dimension. That is:

`[(y_(11),y_(12), . . . , y_(1n)),(y_(21),y_(22), . . . , y_(2n)),(vdots,vdots, ddots , vdots),(y_(m1),y_(m2), . . . , y_(mn))]`

`= [(R_(11),R_(12), . . . , R_(1k)),(R_(21),R_(22), . . . , R_(2k)),(vdots,vdots, ddots , vdots),(R_(m1),R_(m2), . . . ,R_(mk))]xx[(x_(11),x_(12), . . . , x_(1n)),(x_(21),x_(22), . . . , x_(2n)),(vdots,vdots, ddots , vdots),(x_(k1),x_(k2), . . . , x_(kn))]`

Therefore, for a `2xx2` matrix multiplied by a `1xx2`, we have to transpose the vector to get a `2xx1` column vector, giving us an answer that is a `\mathbf(2xx1)` column vector.

Multiplying these two gives:

`[(costheta,-sintheta),(sintheta,costheta)]xx[(-1),(1)]`

`= [(-costheta - sintheta),(-sintheta + costheta)]`

Next, we can plug in `theta = (3pi)/4` (which I'm assuming is the correct angle) to get:

`color(blue)(T(vecx) = R(theta)vecx)`

`= R(theta)[(-1),(1)]`

`= [(-cos((3pi)/4) - sin((3pi)/4)),(-sin((3pi)/4) + cos((3pi)/4))]`

`= [(-cos135^@ - sin135^@),(-sin135^@ + cos135^@)]`

`= [(-(-sqrt2/2) - sqrt2/2),(-sqrt2/2 + (-sqrt2/2))]`

`= color(blue)([(0),(-sqrt2)])`

Now, let's graph this to see what this looks like. I can tell that it's a counterclockwise rotation, after determining the transformed vector.

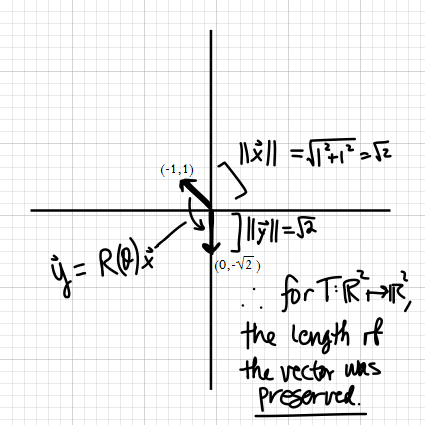
Indeed, a counterclockwise rotation by `135^@`.

CHALLENGE: Maybe you can consider what happens when the matrix is `[(costheta, sintheta),(-sintheta, costheta)]` instead. Do you think it will be clockwise?