Question

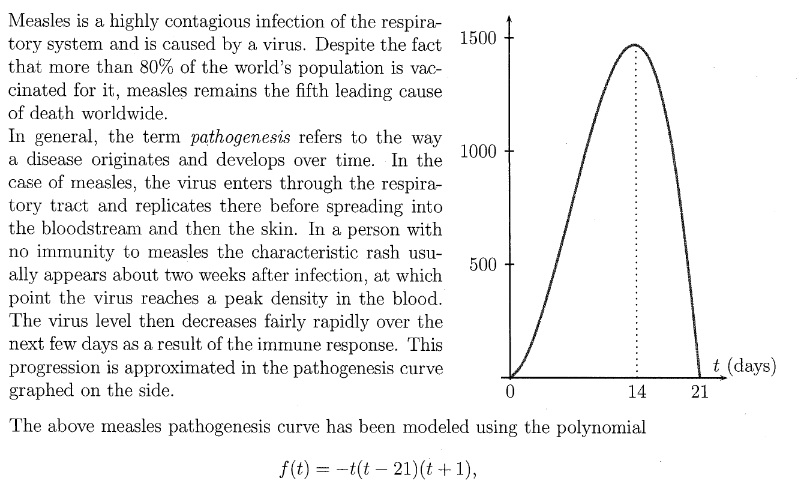
Measles pathogenesis curve by function `f` (see details for questions)?

This question is relevant to Area Between Curves.

I don't know what that constitutes under Socratic guidelines, so it is mentioned here.

A patient infected with the measles virus who has some immunity to the virus has a pathogenesis curve that can be modeled by, for instance, `g(t)=0.9f(t).`

1. If the threshold concentration of the virus required for infectiousness to begin is `"1210 cells/mL"`, on what day does this occur?
2. Let `P_3` be the point on the graph of `g` where infectiousness begins. It has been shown that infectiousness ends at a point `P_4` on the graph of `g` where the line through `P_3`, `P_4` has the slope `-23`. On what day does infectiousness end?
3. Compute the level of infectiousness for this patient.

Answer 1

Hi...this is only an attempt, completely without any (probable) connection with your question....because I didn't know the function `f(t)` so I tried with something I found on the internet!!!

Explanation:

I found on the internet this:
http://www.ms.uky.edu/~ma138/oldexams/Answer_Key_Ex1_S13.pdf

Where `f(t)`is measured in number of infected cells per mL of blood plasma.
In your case should be:

`g(t)=0.9[-t(t-21)(t+1)]`

I tried to plot this function:

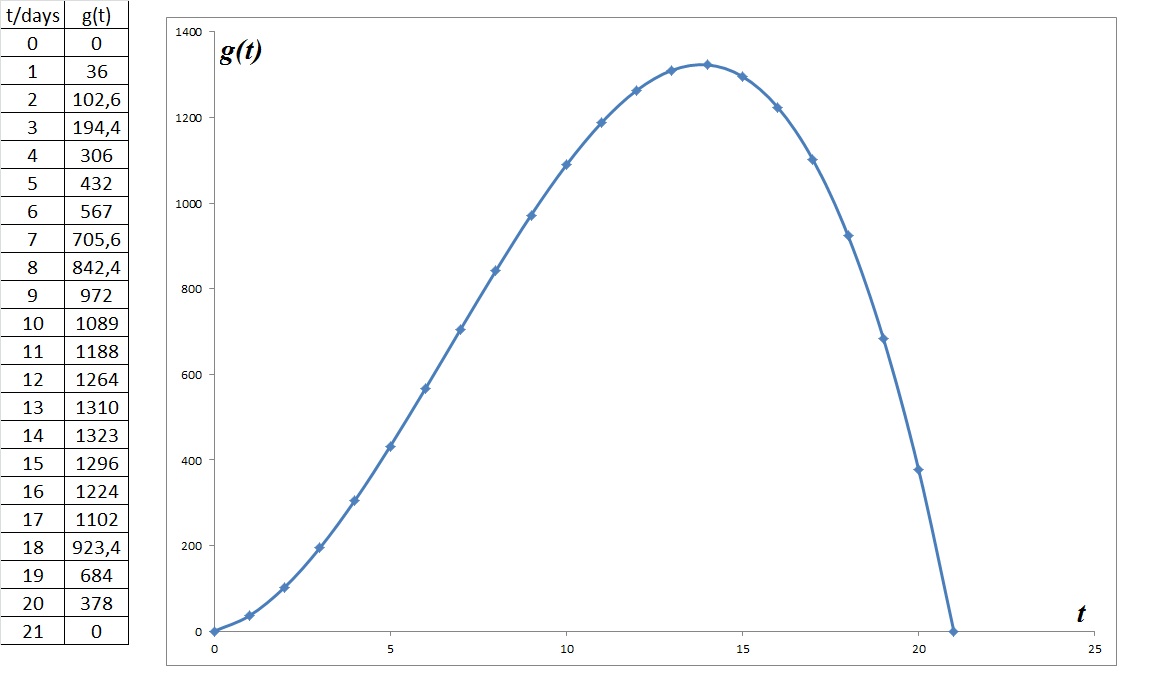
Solving for `g(t)=1210` I got three solutions:
`t_1=11` days
`t_2=-7` days
`t_3=16` days
I think it should be `t_1=11` days that should be the answer to question 1).

To answer question 2) we need a line passing through the above initial point:
`(11, 1210)` and slope `m-23`.
We can use the general relationship from maths:
`y-y_0=m(x-x_0)`
where for us:
`g(t)-1210=-23(t-11)`
`g(t)=-23t+1463`

we can use this line to find the intercepts with:
`g(t)=0.9[-t(t-21)(t+1)]` and get, substituting:
`-23t+1463=0.9[-t(t-21)(t+1)]`
with again three solutions:
`t_1=11` days
`t_2=-8` days
`t_3=17` days
I would choose `t_3=17` days as answer for the end of infectiousness.

for question 3) I do not have any idea at all....sorry!