On August 12, 2000, the Russian submarine Kursk sank to the bottom of the sea, approximately 95 meters below the surface. Can you find the following at the depth of the Kursk?
(a) The water pressure: pressure =
(b) The force on a 4 meter square metal sheet held
Horizontally 95 meters below the surface:
force =
(c) Vertically with its bottom 95 meters below the surface:
force =
(Assume #(g = 9.8 m/s^2)#
I am not sure where to start with this. It feels like I am missing information.
(a) The water pressure: pressure =
(b) The force on a 4 meter square metal sheet held
Horizontally 95 meters below the surface:
force =
(c) Vertically with its bottom 95 meters below the surface:
force =
(Assume
I am not sure where to start with this. It feels like I am missing information.
1 Answer
You coud use Stevin's Law to evaluate the change in pressure at various depths:
Explanation:
You will also need to know the density
Stevin Law:
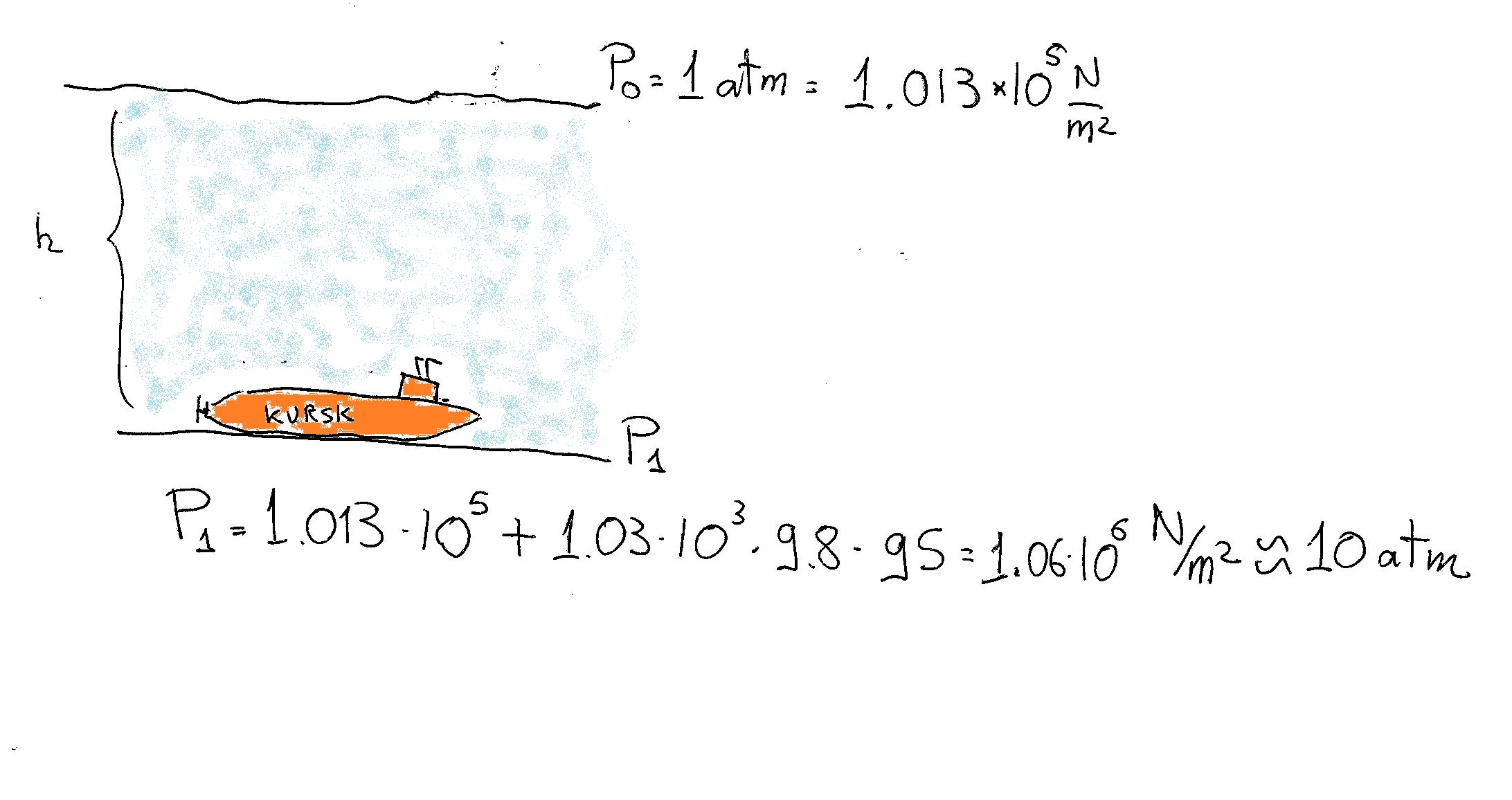
As Pressure is
I supposed the metal sheet area of
The orientation of the metal sheet should not give a big difference; considering a depth of

