Person A travels up in an elevator at uniform acceleration. During the ride, he drops a ball while Person B shoots an arrow upwards directly at the ball. How much time will pass after Person B shot the arrow before the arrow hits the ball?
Person A gets into a construction elevator (it has open sides) at ground level. He is carrying a Styrofoam ball. The elevator starts to travel upwards, accelerating uniformly at a rate of #1.2m/s^2# . After the elevator has been moving #8.0s# , Person A drops the ball over the side of the elevator. The Styrofoam ball, being very light, accelerates downwards at a rate of #3.8m/s^2# . Person B is standing on the ground with a bow and arrow. At the instant when Person A drops the Styrofoam ball, Person B shoots an arrow upwards at a speed of #32m/s# directly at the ball. How much time will pass after Person B shot the arrow before the arrow hits the ball?
Person A gets into a construction elevator (it has open sides) at ground level. He is carrying a Styrofoam ball. The elevator starts to travel upwards, accelerating uniformly at a rate of
4 Answers
This solution is not really valid. Please see the other solutions which are better.
Explanation:
I will consider the problem in two phases. The first phase is the motion of the elevator before the ball is dropped, the second phase is after the ball is dropped and the arrow is shot upward.
Phase 1: Elevator accelerating upwards.
Acceleration is constant so we can use an equation of constant acceleration to determine the height, h, from which the ball will be dropped.
Use this equation:
Phase 2: Ball dropped from elevator.
In this solution I will assume that the ball is dropped with zero initial velocity. However, because the elevator has an upward velocity of
Furthermore, I believe that the question implies we should make that assumption because it states that the ball "accelerates downwards with acceleration of
So after
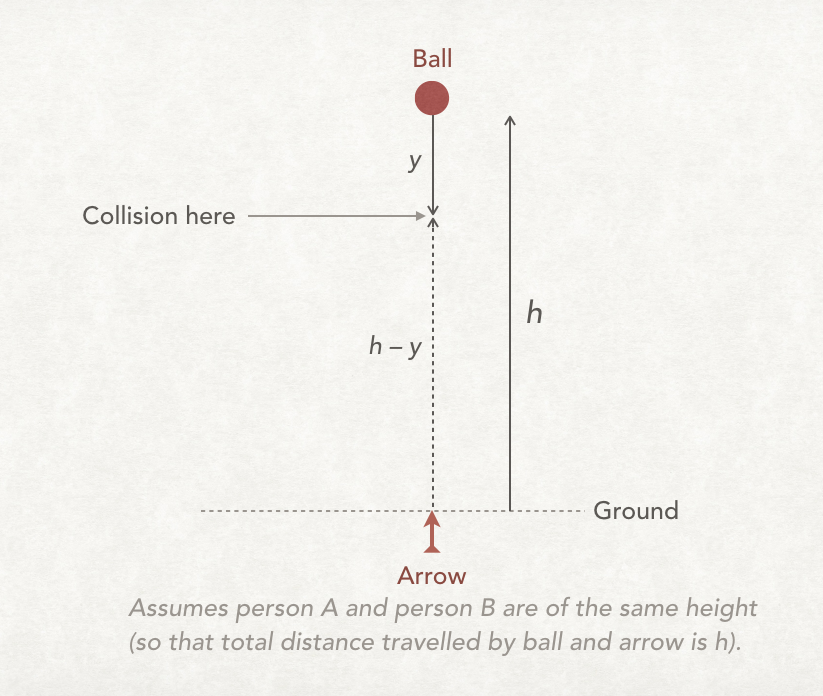
Now apply the equations of constant acceleration to the ball, then to the arrow and then use simultaneous equations to solve for t. In both cases we will use the equation:
Ball
Equation ①:
Arrow
Equation ②:
Equation ① = Equation ②:
Factorise the quadratic to find solutions for t:
The solution that we want for this problem is
So the solution is
We can check this solution by passing the value of t back into equations ① and ②.
Equation ① :
Equation ② :
As you can see the two values for y are consistent, so the value of t should be accepted.
Without assuming that the ball starts with zero initial velocity the time taken would be:
Explanation:
Plot spoiler: I do not assume that the ball is released with zero initial velocity in this solution. This is a long solution with some fairly complex assumptions, it is not for the faint hearted!
I will consider the problem in three parts. The first part is the motion of the elevator before the ball is released, the second part is between the ball being released and reaching its maximum height, and the third part is between the ball starting to fall downwards and the arrow colliding with the ball.
Part 1: Elevator accelerating upwards.
Acceleration is constant so we can use an equation of constant acceleration to determine the height, h, at which the ball will be released.
Use this equation:
We also need to know the velocity of the elevator at this height as the ball will have this as its initial velocity:
Part 2: Ball released from elevator.
The ball is released with an upward velocity of
The situation is shown in the diagram below.
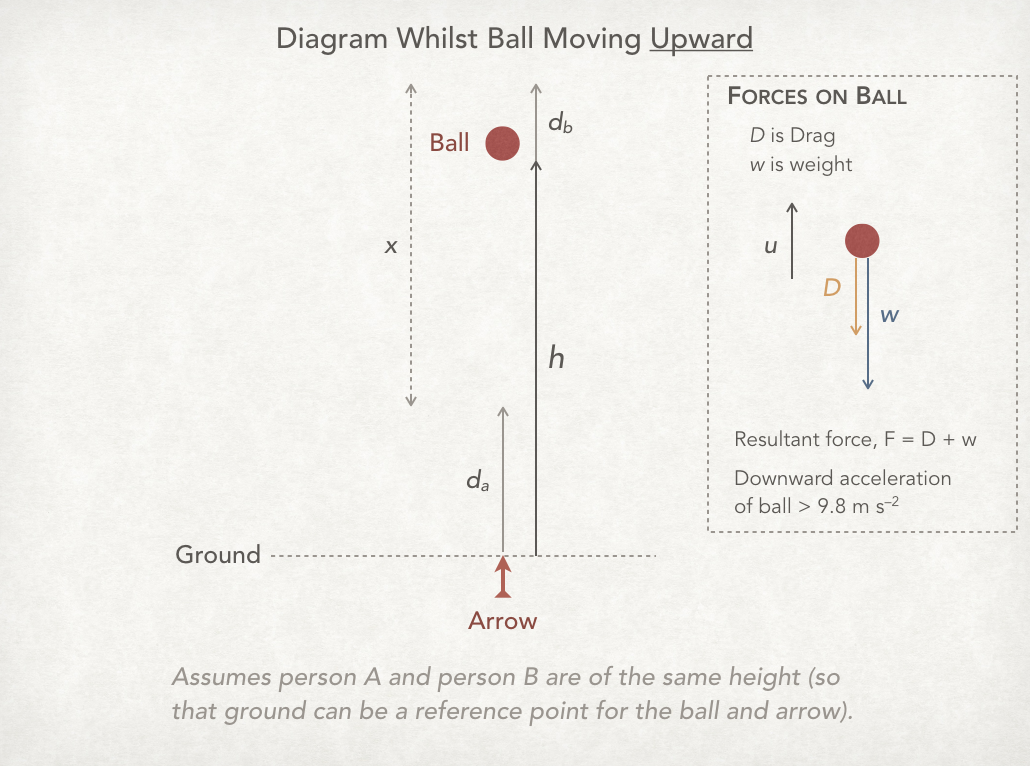
An important note about how I have treated drag in this solution.
The question does not give us sufficient information to correctly handle drag in this question. Drag is a function of velocity squared, so the drag in reality would increase as the ball accelerated and vice versa. But the question gives us a fixed value of the acceleration of the ball whilst it is moving downwards (
So I have made the following assumptions in order to write something that gets as close as possible to a proper solution:
1. The drag does not change as a function of velocity squared.
2. The value of the acceleration due to drag is constant in all cases. When the ball is going down drag changes the acceleration from
3. The ball does not reach terminal velocity in either aspect of its motion.
Height of the Ball and Time of Travel:
If you notice in the diagram I drew the forces acting on the ball. Whilst it is travelling upwards drag and weight act downwards. So the accelerations due to them both will be added together to find the resultant acceleration. Noting the above assumptions the upward deceleration is
For the height use this equation:
For the time of travel use this equation:
Don’t forget to add this time to what is calculated in part 3.
How far the arrow travelled during this time and its final velocity:
For the height use
For the final velocity use
So when the ball reaches maximum height the distance between ball and arrow, x, is:
Part 3: From ball starting to drop downwards to collision.
The situation now is as shown in the diagram below. The total distance between ball and arrow is x and the ball falls through distance y before colliding with the arrow. So the arrow therefore moves through distance x – y before colliding with the ball.
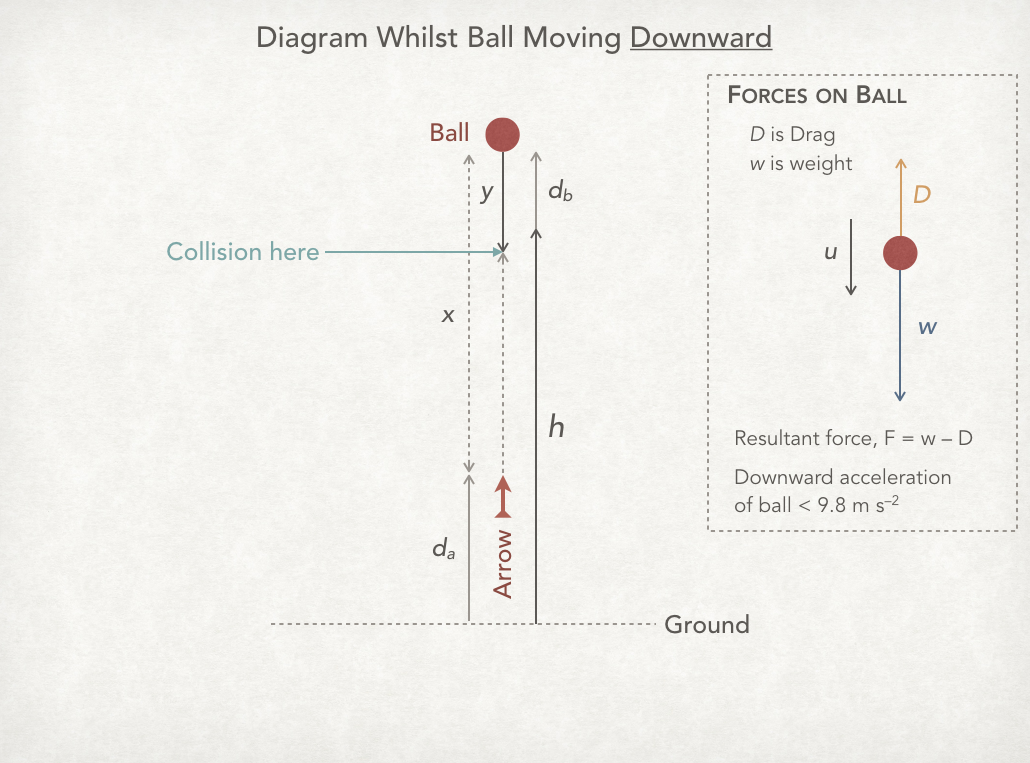
Now apply the equations of constant acceleration to the ball, then to the arrow and then use simultaneous equations to solve for t. In both cases we will use the equation:
Ball
Equation ①:
Arrow
Equation ②:
Substitute for y in equation ②:
Factorise the quadratic to find solutions for t:
The solution that we want for this problem is
So our solution is
Now add to that the time calculated in part 2 to give the final solution:
We can check the quadratic solutions by passing the value of t back into equations ① and ②.
Equation ① :
Equation ② :
As you can see the two values for y are consistent, so the value of t should be accepted.
8/3s
Explanation:
The elevator starts with initial velocity Zero and with acceleration
also attains velocity,
At this moment (just completion of 8s) the person A drops the ball and person B shoots the arrow from the ground with initial upward velocity,
Let after
During this ts if arrow ascends height
Then
Again during this t s if the ball ball ascend
Obviously
So subtracting Eq (2) from Eq (1) we can write
smallest value of t
If the arrow bypasses the ball without hitting then second meeting is possible and the second value of t = 4.8 s is the time of second crossing when both ball and arrow move downward in the back journey
To add to existing solutions, here is one more.
Explanation:
The problem is dealt in two time-phases.
- The person with Styrofoam ball travels up in the elevator.
Elevator equation. Let us take up as#+ve# direction. Given that
#u = 0 #
#a = 1.2 m.s^(-2)#
#t = 8.0s#
We need to ascertain what was the velocity
Using the equation
Using
- Ball dropped from the elevator and simultaneously arrow shot from the ground.
Arrow.
Suppose the arrow hits the ball after
Given
Using
Ball.
Given and calculated for the ball.
Using
To make an assessment when and where does the arrow hit the ball.
(a) Time
Using
or
Height
Total height from the ground of ball at this point
Height at the point of drop
Distance traveled by arrow during this period. put
(b) It is clear that the arrow hits the ball only when it has started its downward journey from the position of highest point.
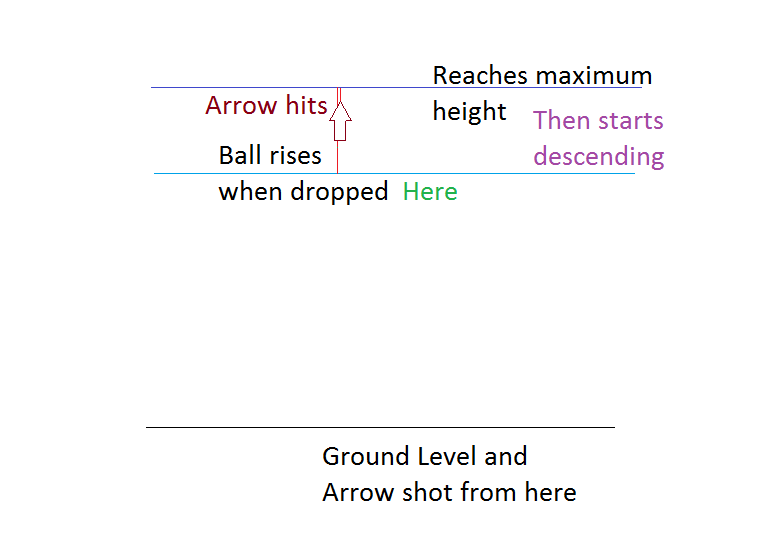
Let the arrow hit the ball after elapse of time
This can be found from (1) as
The ball moves down in this duration to meet the arrow
Using
Inserting value of
Ignoring
When the ball is dropped. Three main forces come into play.
1. Gravity, downwards
2. Buoyancy, upwards
3. Drag, initially downwards; from the point of drop to the point when ball reaches maximum height. Thereafter upwards when the ball starts descent. Always opposite to the direction of velocity.
Per very fine analysis recently shared by fellow contributor Daniel W., contribution due to the buoyancy of Styrofoam in air is negligible as the density of Styrofoam varies from
The statement of the question is silent about the drag. Keeping in with this drag has been treated as ignored.
We also know that
Drag
Drag
In the instant case, keeping in view, the constant of proportionality, density of air, area of cross-section of the ball, decreasing magnitude of velocity upwards and very low value of velocity when the arrow hits the ball when it is descends could make a good case for ignoring Drag in comparison to Gravity.
There appears no real life justification for choosing such a low value of acceleration of the ball after dropping from the elevator.


