Phosporous-32 is a radioisotope used in molecular biology After 44 days, 17% of the sample remains. How do you calculate the half-life?

Question

1759 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-05T22:19:17

You can do it like this:

The expression for 1st order decay is:

#sf(N_t=N_0e^(-lambdat))#

#sf(lambda)# is the decay constant.

The graph looks like this:

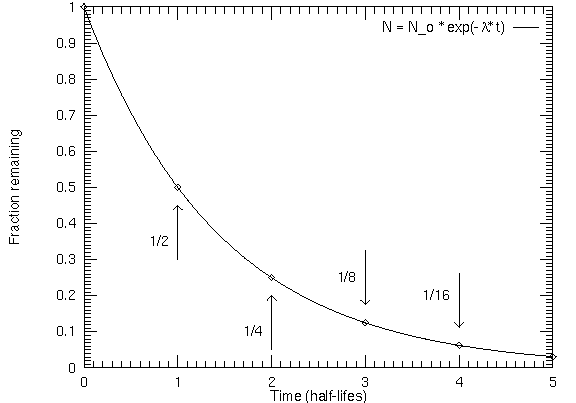
www.astronomynotes.com

The key to the problem is to find the decay constant #sf(lambda)# as this is directly related to the 1/2 life.

Taking natural logs of both sides gives:

#sf(lnN_t=lnN_0-lambdat)#

If we assume we start with 100 undecayed atoms this becomes:

#sf(ln17=ln100-lamdaxx44)#

#:.##sf(2.833=4.605-lamdaxx44)#

#:.##sf(lambda=1.772/44=0.0403color(white)(x)d^(-1))#

This is related to the 1/2 life by:

#sf(t_(1/2)=0.693/lambda=0.693/0.0403=17color(white)(x)d)#