Question

If each orbital can hold a maximum of 3 electrons, the number of elements in the 4th `bb"[period of the]"` periodic table (long form) is?

In brackets is a fix to the question.
- Truong-Son

Answer 1

Well, this is kind of open to interpretation... but if I interpreted it correctly, I get `27` elements, compared to the original `18` elements, in the 4th period of the periodic table.

(If you already knew that the number of electrons allowed in a given orbital is derived from the properties of electrons, and NOT of the orbitals themselves, the answer quickly follows.)

---

PRELIMINARY THINGS

I think there's a typo in the question... I looked this up elsewhere, and it's probably...

If each orbital can hold a maximum of 3 electrons, the number of elements in the 4th period of the periodic table (long form) is...?

Also, note that this is entirely theoretical, as all electrons only have two possible spins (`m_s = pm1/2`) in a given orbital, and no two electrons can share the same quantum state (Pauli Exclusion Principle); that restricts each orbital to contain only two electrons in real life.

That aside, when we suppose three electrons are "allowed" in a single orbital (assuming the other three quantum numbers are as normal), we suddenly "allow" `50%` more elements in a given quantum level.

(It's not really why the periodic table was arranged historically, but... I suppose that's what the intent of this question was...)

EXPANDING THE PERIOD...

An electron configuration for the fourth period in a generalized manner is written as:

`4s^x 3d^x 4p^x`

where:

• `x = (2l+1) cdot N_(m_s)` is the total number of electrons in all the orbitals in a given subshell.
• `l` is the angular momentum quantum number. `l = 0, 1, 2, 3, . . .` corresponds to `s, p, d, f, . . .` orbitals.
• `2l+1` is known as the degeneracy of the subshell; it is how many orbitals are in that subshell.
• `N_(m_s)` is an arbitrary number of spins the electron could have, as it also then gives the maximum number of electrons per orbital. In this case we SUPPOSE that `N_(m_s) = 3`, but in real life it is just `2`.

Now, the number of allowed `m_s` values derives from the properties of the electron, not of the orbitals themselves, so having more spins allowed does NOT change the orbital shapes or relative energies.

For the `4s` orbital:

`l = 0, => 2l+1 = 1`

For the `3d` orbitals:

`l = 2, => 2l+1 = 5`

For the `4p` orbitals:

`l = 1, => 2l+1 = 3`

Thus, the hypothetical electron configuration we would then write is...

`4s^(1cdot3) 3d^(5 cdot 3) 4p^(3 cdot 3)`

`= 4s^3 3d^15 4p^9`

And that would apparently expand the fourth period of the periodic table from `18` elements to `color(blue)(27)` elements.

Answer 2

This is what I get.

Explanation:

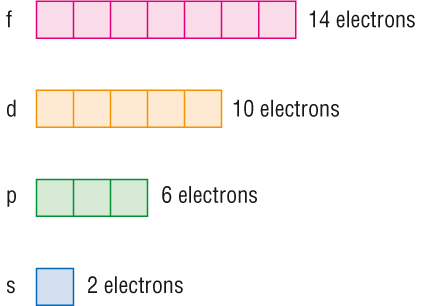
We see that on the assumption that each orbital holds maximum of `2` electrons, for `4th` period, `n=4` allowed orbitals are `s,p,d andf`

`s` orbital holds `2` electrons

`p` orbital holds `6` electrons

`d` orbital holds `10` electrons

`f` orbital holds `14` electrons

Total number of electrons held in `n=4` shell, `=32` electrons.

If each orbital is allowed to hold `3` electrons.

Total number of electrons held in this shell `=32/2xx3=48` electrons.

This is the number of elements allowed in `4th` period.
.-.-.-.-.-.-.-.-.-.-.-.-.-.-

Alternatively

`s` orbital holds `3` electrons

`p` orbital holds `9` electrons

`d` orbital holds `15` electrons

`f` orbital holds `21` electrons

Total number of electrons `=3+9+15+21=48`