Points (6 ,7 ) and (5 ,5 ) are (2 pi)/3 radians apart on a circle. What is the shortest arc length between the points?
1 Answer
Mar 11, 2016
Explanation:
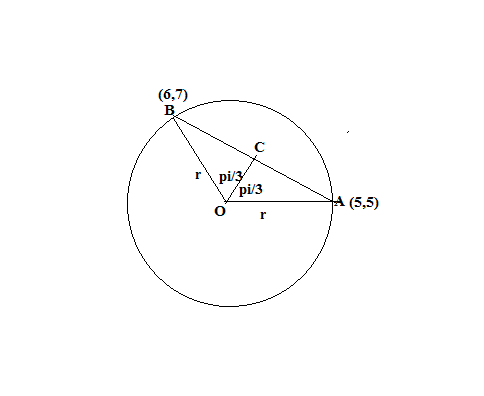
AB =
Let radius of circle =r
arc length =

