Distance between #(7,1)# and #(8,9)# is given by the Pythagorean Theorem as
#color(white)("XXX")sqrt(1^2+8^2)=sqrt(65)#
To determine the arc length we will need to determine the radius of a circle with the given points at an angle of #(3pi)/4# relative to the center of the circle.
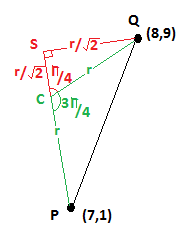
(Note this diagram is not accurate).
If we let the radius of this circle be #color(green)(r)#
and denote
#color(white)("XXX")(7,1)# as #P#,
#color(white)("XXX")(8,9)# as #Q#,
#color(white)("XXX")#the center of the circle as #C#, and
#color(white)("XXX")#the point on the extension of #PC# to form a right angle with #Q# as #S#
then
Since
#color(white)("XXX")/_PSQ=pi/2#, and
#color(white)("XXX")/_QCS=pi-(3pi)/4=pi/4#
#rarr#
#color(white)("XXX")/_CQS=pi/4# and
#color(white)("XXX")abs(CS)=abs(QS)=r/sqrt(2)#
Therefore
#color(white)("XXX")abs(PS)=r+r/sqrt(2)=((sqrt(2)+1)/sqrt(2))r#
and
#color(white)("XXX")abs(PQ)=sqrt((r/sqrt(2))^2+(((sqrt(2)+1)/(sqrt(2)))r)^2)#
#color(white)("XXX")=(sqrt(2+sqrt(2)))r#
But we previously determined that
#color(white)("XXX")abs(PQ)=sqrt(65)#
So
#color(white)("XXX")r=sqrt(65)/(sqrt(2+sqrt(2))#
The shortest arc length of an arc with radius #color(green)(r)# and an angle of #(3pi)/4# is #3/4r#
#rArr # shortest arc length is #3/4xxsqrt(65)/(sqrt(2+sqrt(2)))#
#color(white)("XXX")=(3sqrt(65))/(4sqrt(2+sqrt(2)))#

