Help Me With These Simple Formulae Questions?
Hi all, first of all I'd like to thank you for your time. Please answer all three of these questions below in as much detail as you can also including detailed steps. Thank you!
Question 7 & 8

Question 8 (Review Set)
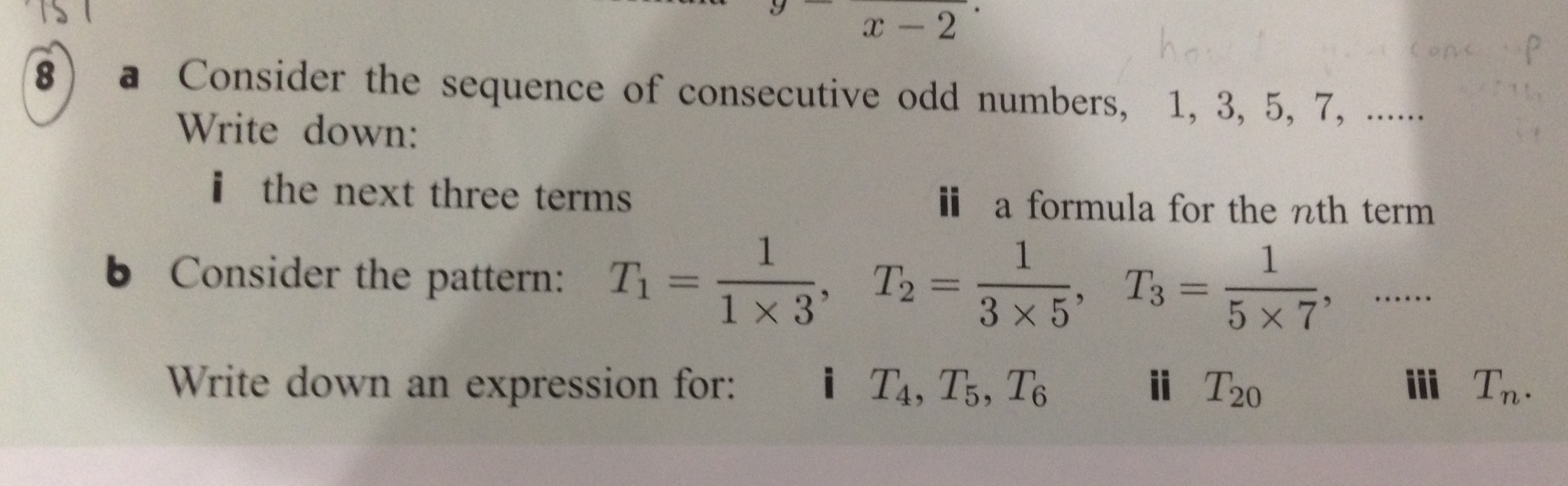
Hi all, first of all I'd like to thank you for your time. Please answer all three of these questions below in as much detail as you can also including detailed steps. Thank you!
Question 7 & 8

Question 8 (Review Set)
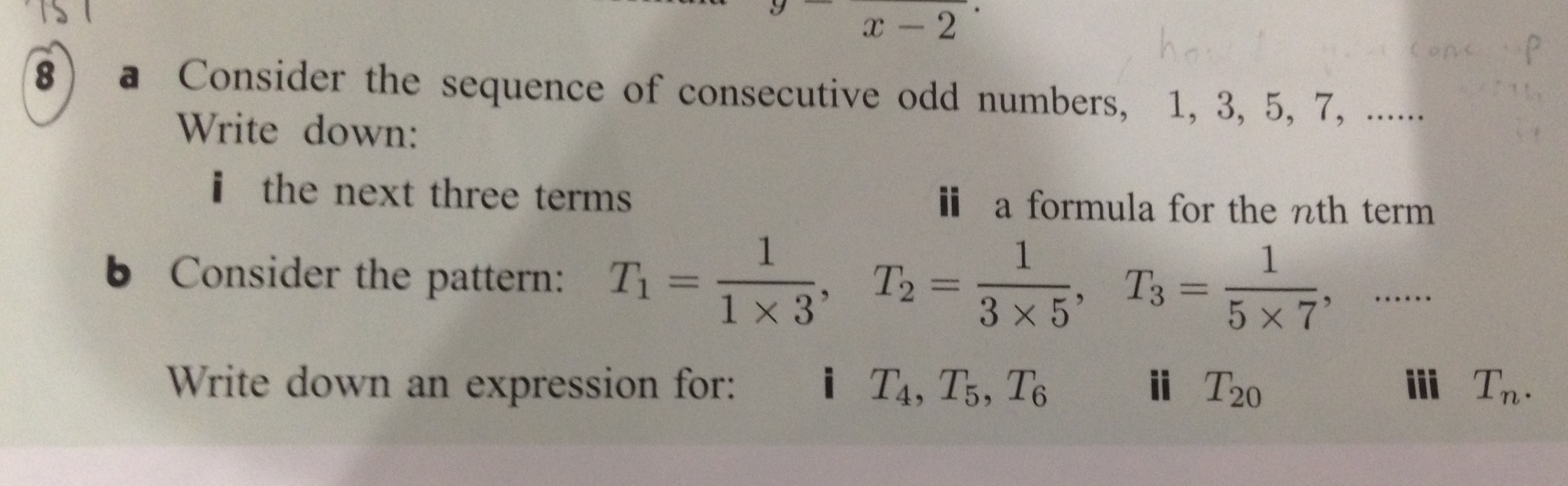
3 Answers
Question "7" - see below:
Explanation:
For the question "7":
solve for
~~~~~
When
When
Question "8" - see below:
Explanation:
Question "8"
Solve for
~~~~~
Find
~~~~~
Find
Review Set 8 - see below:
Explanation:
Review Set 8:
With the set of consecutive odd integers, we are given:
The next 3 terms are:
The
For the pattern of
where
following the pattern:
notice that, in the denominator, the smaller of the two numbers is the
Hence, for the 20th term, we'll have the lesser term in the denominator as:
and therefore:
and

