Question

Sketch the velocity-time graph for two particles colliding in vertical motion?

Two points A and B are located on a vertical line with point A vertically above point B. A particle is released from rest at A and at the same time another particle is projected vertically upwards from B at velocity `v`. The particles collide when the top one has fallen a distance `y`.
The height of point A above point B is `h`.
If `h=100m`, `v=20 ms^-1` and `g=10 ms^-2`, sketch the velocity-time graph, and mark on the graph the `(t,v)` values where the particles collide. Take `v` to be positive upwards.

An earlier part of the question also had you showing that the time to collision was `t=h/v`

Answer 1

Let,after time `t` there will be collision between the two particles,

So,for the one,coming down in that time if comes down by distance `x`,we can write,

`y=1/2g t^2`...1

so, for the one going up,we can write,

`100-y = 20t - 1/2g t^2`

or, `100 -1/2g t^2 = 20 t -1/2 g t^2`(from 1)

so, `t=100/20 = h/v=5 s` (given, `h=100` and `v=20`)

Now,equation of velocity time relationship for the particle going up is `v'=v-g t=20 -10t` (taking upward positive)

and, for the one going down is `v=-g t=-10t`

So,when both will meet,the velocity of th one going down will be `-10*5=50 m/s` and the one going up will be `20-10*5=30 m/s`

Now,these things are plotted to make a graph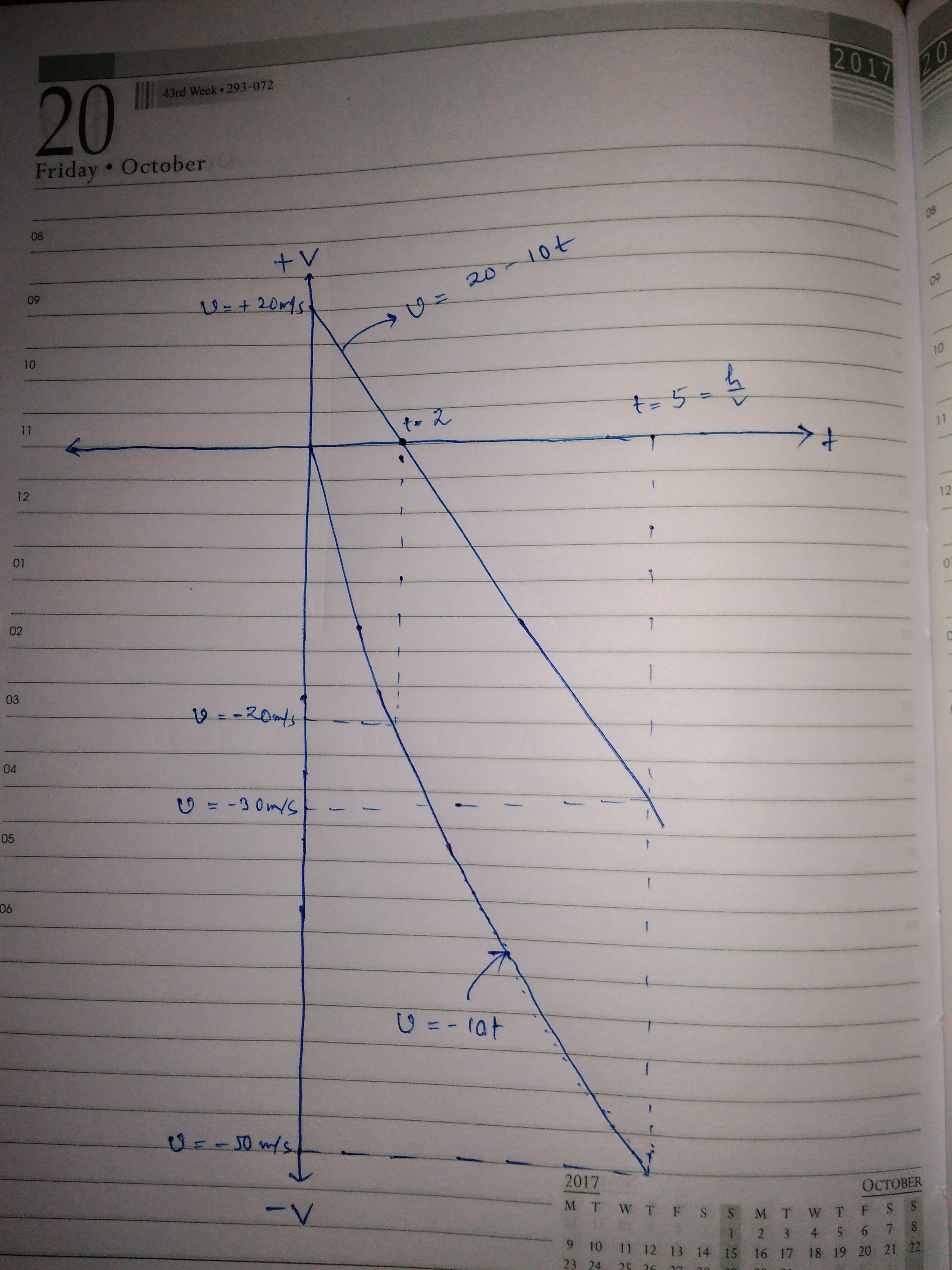

Sorry for the drawing got excessively enlarged,but I have tried to mark velocities of the two particles for important time values.

Note, at `t=2` the particle going up comes to rest,but the one going down has a velocity of `-10*2=-20 m/s` (downwards)