Solve this problem? It's so hard for me
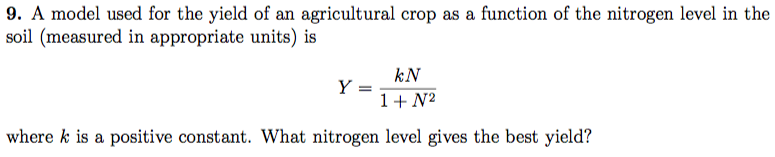
2 Answers
Nitrogen level of
Explanation:
As yield
it is maximized when
As
=
It is
Further
When
Hence nitrogen level of
The best yield will be when
Explanation:
I have no idea how plants work but I'm assuming the more nitrogen a plant has the better. Therefore we are looking for maximum. We can find that by first derivative: (k is constant)
min:
max:
The best yield will be when

