Question

Suppose the diameter of a circle is 30 centimeters long and a chord is 24 centimeters long. How do you find the distance between the chord and the center of the circle?

Answer 1

9 cm.

Explanation:

If AB is the chord, M is its midpoint and C is the center of the circle,
the distance between the chord and the center is `CM = sqrt((CA)^2-(AM)^2)=sqrt(15^2-12^2)=sqrt81=9`
CA = radius of the circle = 15 cm and AM = (length of the chord)`/`2 = 12 cm

Answer 2

`9cm`

Explanation:

Consider the image

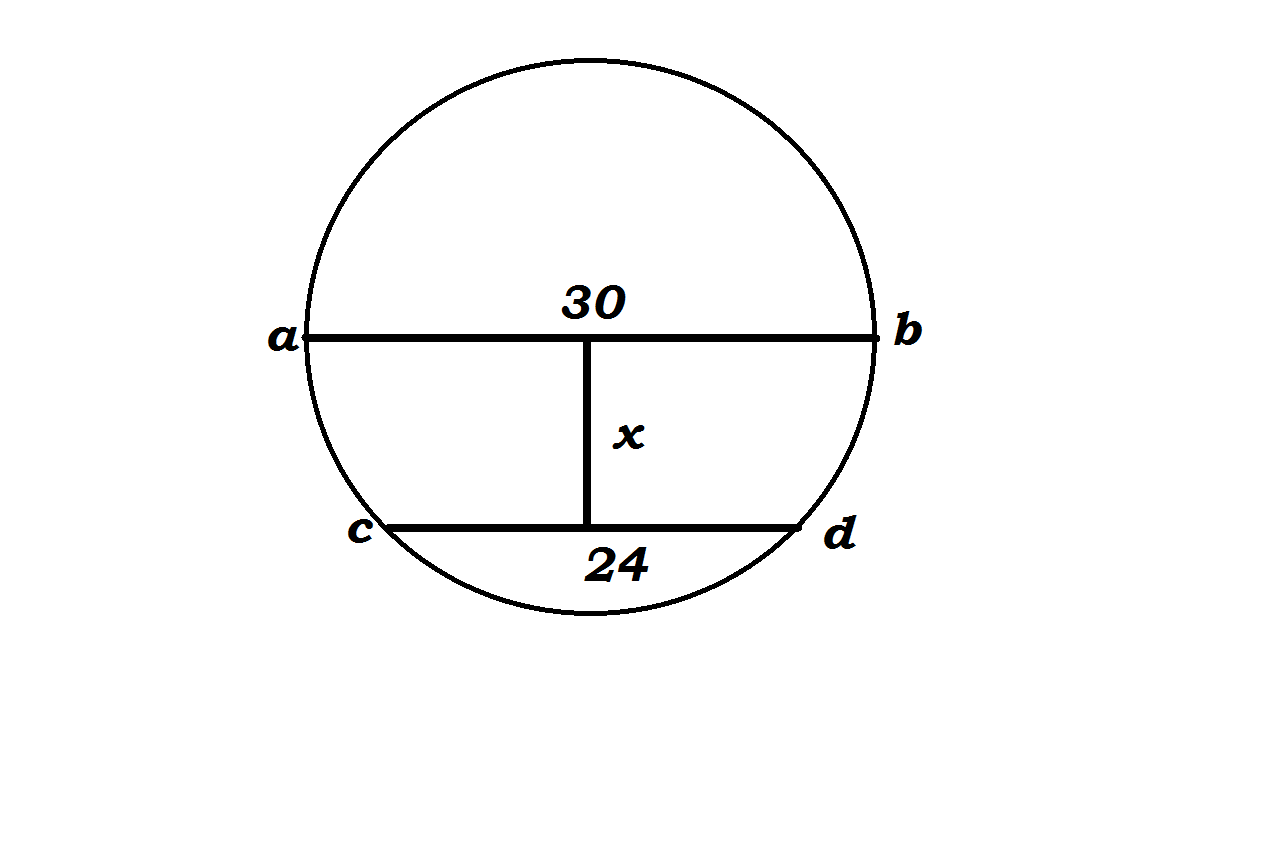
Let the distance between the chord and centre of the circle be `x`

We need to find `x`

For that we need to recreate this image

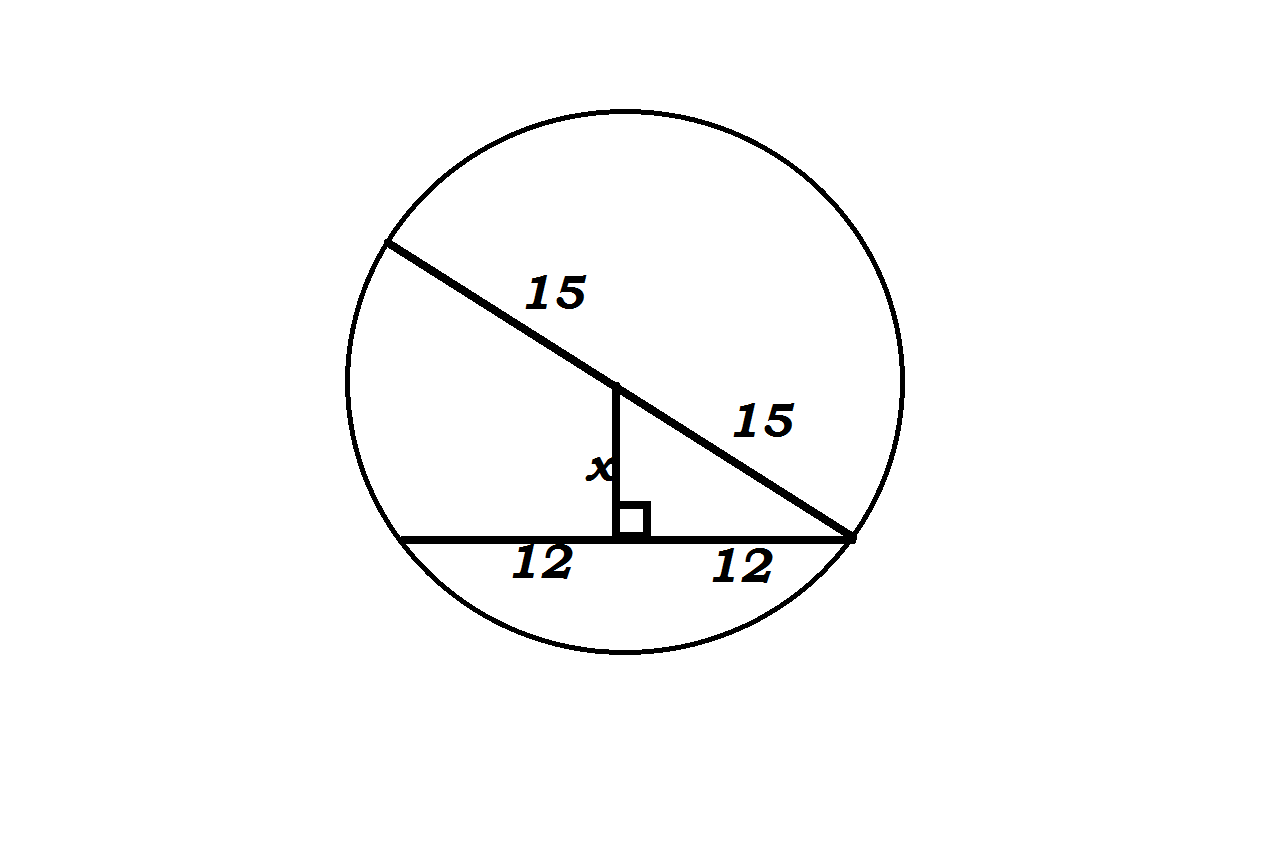
Now we have formed a right angle triangle

Now the problem has become easy!

Use Pythagoras theorem

`color(blue)(a^2+b^2=c^2`

Where,

`aand b` are the right containing sides (`xand12`)

`c` is the Hypotenuse (longest side-`15`)

`rarrx^2+12^2=15^2`

`rarrx^2+144=225`

`rarrx^2=225-144`

`rarrx^2=81`

`color(green)(rArrx=sqrt81=9`