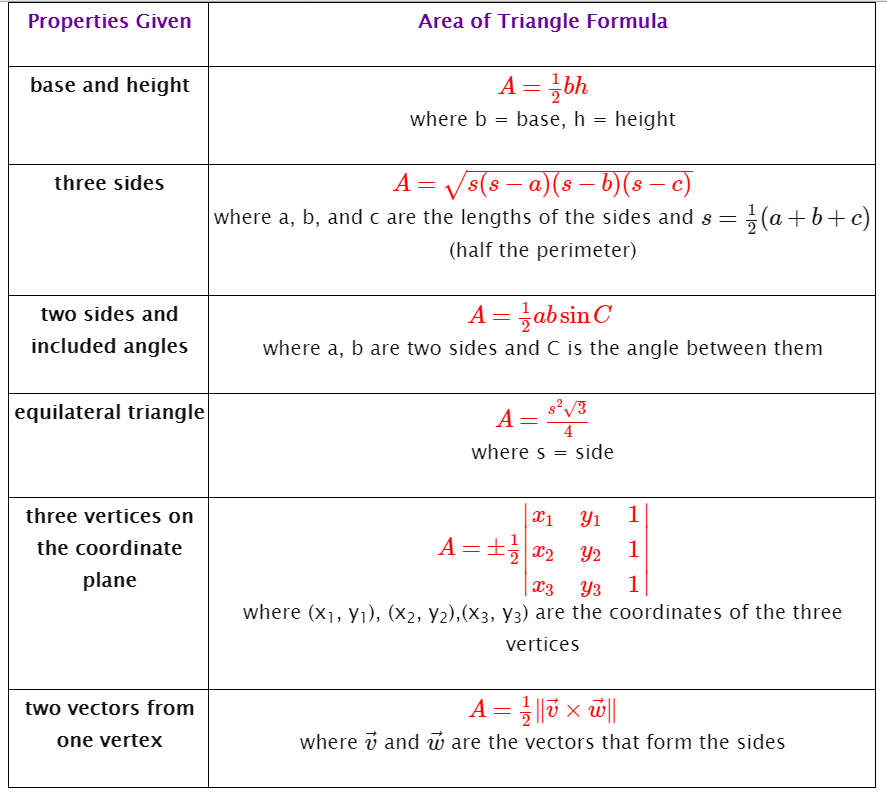
The base of a triangular pyramid is a triangle with corners at (3 ,8 )(3,8), (1 ,6 )(1,6), and (2 ,8 )(2,8). If the pyramid has a height of 4 4, what is the pyramid's volume?

2 Answers
Pretish
Jun 9, 2018

\frac{8}{3}83 units^2

Explanation:

The area of the base (triangle) can be worked out from the vertices, as

Area = {2 * 2}{2} = 2{2⋅2}{2}=2

Therefore by using the formula

V = {A * h}{3}V={A⋅h}{3} we get the volume as \frac{2*4}{3} = \frac{8}{3}2⋅43=83

sankarankalyanam
Jun 10, 2018

color(blue)("Volume of a pyramid "V_p = 1/3*A_b*h=1/3 *1*4 = 4/3 Volume of a pyramid Vp=13⋅Ab⋅h=13⋅1⋅4=43

Explanation:

https://www.onlinemathlearning.com/area-triangle.html

"Area of triangle knowing three vertices on the coordinate plane is given by "Area of triangle knowing three vertices on the coordinate plane is given by

color(crimson)(A_b = |1/2(x_1(y_2−y_3)+x_2(y_3−y_1)+x_3(y_1−y_2))|Ab=∣∣∣12(x1(y2−y3)+x2(y3−y1)+x3(y1−y2))∣∣∣

(x_1,y_1)=(3,8) ,(x_2,y_2)=(1,6),(x_3,y_3)=(2,8) , h=4(x1,y1)=(3,8),(x2,y2)=(1,6),(x3,y3)=(2,8),h=4

A_b = |1/2(3(6−8)+1(8−8)+2(8−6))| = 1Ab=∣∣∣12(3(6−8)+1(8−8)+2(8−6))∣∣∣=1

color(crimson)("Volume of a pyramid " V_p = 1/3* A_b * hVolume of a pyramid Vp=13⋅Ab⋅h

color(blue)("Volume of a pyramid "V_p = 1/3*A_b*h=1/3 *1*4 = 4/3 Volume of a pyramid Vp=13⋅Ab⋅h=13⋅1⋅4=43

Related questions
See all questions in Volume of Solids
Impact of this question
2678 views around the world
You can reuse this answer
Creative Commons License