The base of a triangular pyramid is a triangle with corners at #(4 ,2 )#, #(3 ,6 )#, and #(7 ,5 )#. If the pyramid has a height of #8 #, what is the pyramid's volume?

2 Answers
George C.
Oct 18, 2017

#20#

Explanation:

The triangle with vertices #(4, 2)#, #(3, 6)# and #(7, 5)# can be drawn inside a #4 xx 4# square with vertices #(3, 2)#, #(7, 2)#, #(7, 6)# and #(3, 6)#, dividing it into #4# triangles...

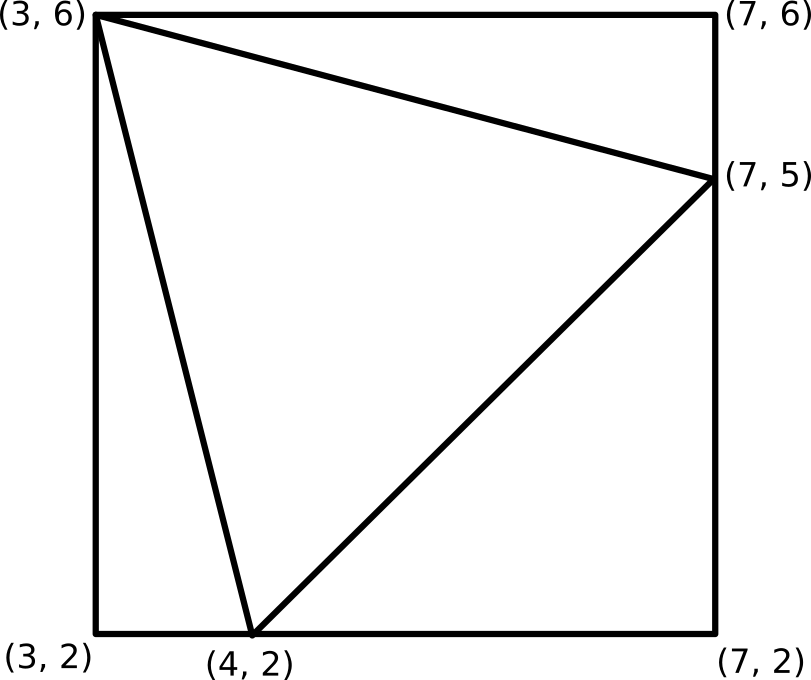
enter image source here

The two smaller triangles are right angled triangles with legs of lengths #1# and #4#, so their total area is #4#.

The larger isosceles right angled triangle has area #1/2 * 3 * 3 = 9/2#

So the total area of the given triangle is:

#4^2 - 4 - 9/2 = 15/2#

The pyramid has volume:

#1/3 * "base" * "height" = 1/3 * 15/2 * 8 = 20#

George C.
Oct 18, 2017

#20#

Explanation:

The area of a triangle with vertices #(x_1, y_1)#, #(x_2, y_2)#, #(x_3, y_3)# is given by the formula:

#"Area" = 1/2 abs(x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2)#

(see https://socratic.org/s/aK6h7PjW)

So putting:

#{ ((x_1, y_1) = (4, 2)), ((x_2, y_2) = (3, 6)), ((x_3, y_3) = (7, 5)) :}#

we find that the base of our pyramid has area:

#1/2 abs((4)(6)+(3)(5)+(7)(2)-(4)(5)-(3)(2)-(7)(6))#

#=1/2 abs(24+15+14-20-6-42)#

#=1/2 abs(-15)#

#=15/2#

Then the volume of the pyramid is:

#1/3 xx "base" xx "height" = 1/3 * 15/2 * 8 = 20#

Related questions
See all questions in Volume of Solids
Impact of this question
2633 views around the world
You can reuse this answer
Creative Commons License