The base of a triangular pyramid is a triangle with corners at #(4 ,2 )#, #(3 ,6 )#, and #(7 ,5 )#. If the pyramid has a height of #8 #, what is the pyramid's volume?
2 Answers
Explanation:
The triangle with vertices
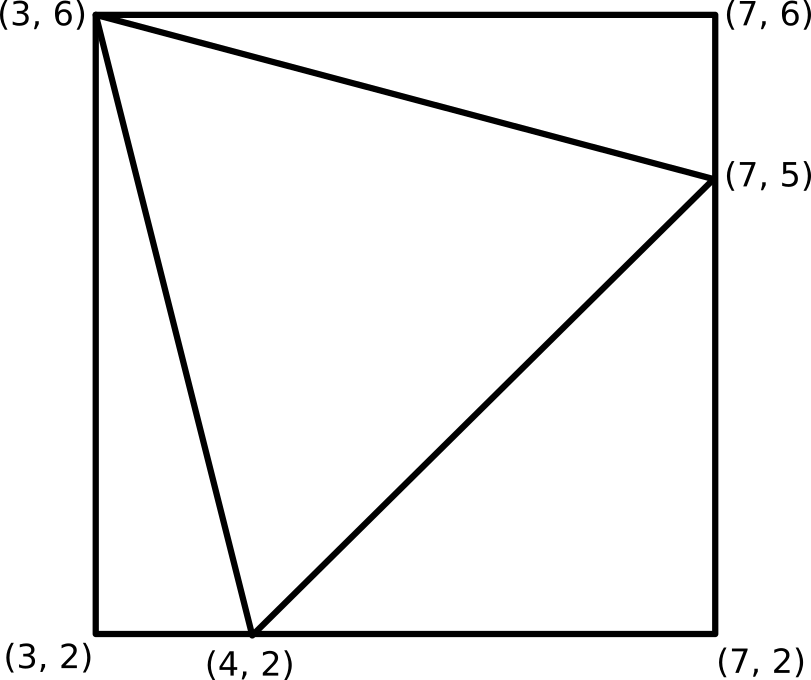
The two smaller triangles are right angled triangles with legs of lengths
The larger isosceles right angled triangle has area
So the total area of the given triangle is:
#4^2 - 4 - 9/2 = 15/2#
The pyramid has volume:
#1/3 * "base" * "height" = 1/3 * 15/2 * 8 = 20#
Explanation:
The area of a triangle with vertices
#"Area" = 1/2 abs(x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2)#
(see https://socratic.org/s/aK6h7PjW)
So putting:
#{ ((x_1, y_1) = (4, 2)), ((x_2, y_2) = (3, 6)), ((x_3, y_3) = (7, 5)) :}#
we find that the base of our pyramid has area:
#1/2 abs((4)(6)+(3)(5)+(7)(2)-(4)(5)-(3)(2)-(7)(6))#
#=1/2 abs(24+15+14-20-6-42)#
#=1/2 abs(-15)#
#=15/2#
Then the volume of the pyramid is:
#1/3 xx "base" xx "height" = 1/3 * 15/2 * 8 = 20#

