The base of a triangular pyramid is a triangle with corners at #(4 ,2 )#, #(3 ,7 )#, and #(5 ,3 )#. If the pyramid has a height of #5 #, what is the pyramid's volume?
2 Answers
Volume of pyramid
Explanation:
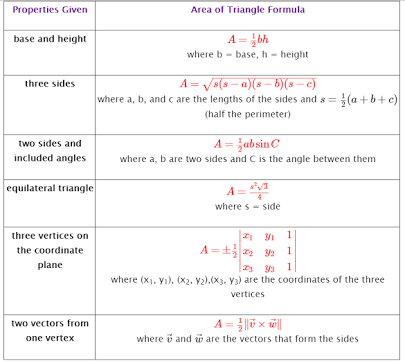
First to find the area of the triangular base.
If three sides are known, area of the triangle is given by the formula
where s is the semi perimeter of the triangular base, a,b and c the sides of the base.
Using distance formula we can find the sides.
Semi perimeter
Area of triangular base
Volume of pyramid
Explanation:
#"the volume (V) of a pyramid is calculated using the formula"#
#•color(white)(x)V=1/3xx"area of base "xx"height"#
#"the area of the base (A) can be found using"#
#•color(white)(x)A=1/2|x_1(y_2-y_3)+x_2((y_3-y_1)+x_3(y_1-y_2)|#
#"let "(x_1,y_1)=(4,2),(x_2,y_2)=(3,7),(x_3,y_3)=(5,3)#
#A=1/2|4(7-3)+3(3-2)+5(2-7)|#
#color(white)(A)=1/2|16+3-25|=3#
#rArrV=1/3xx3xx5=5#

