The base of a triangular pyramid is a triangle with corners at #(4 ,4 )#, #(3 ,2 )#, and #(5 ,3 )#. If the pyramid has a height of #5 #, what is the pyramid's volume?
1 Answer
Jan 8, 2018
Volume of pyramid
Explanation:
The shoelace formula or shoelace algorithm (also known as Gauss's area formula and the surveyor's formula[1]) is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their Cartesian coordinates in the plane.
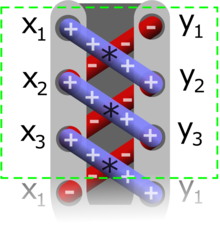
Using shoelace formula to find the area of the given triangle base :
Volume of pyramid
