The base of a triangular pyramid is a triangle with corners at (6 ,5 ), (2 ,4 ), and (4 ,7 ). If the pyramid has a height of 2 , what is the pyramid's volume?
1 Answer
Mar 2, 2016
Explanation:
The volume of a pyramid is given by
so the first step is to find the area of the base.
The simplest way to do that, given the three vertices, is to find the lengths of the three sides and use the area formula
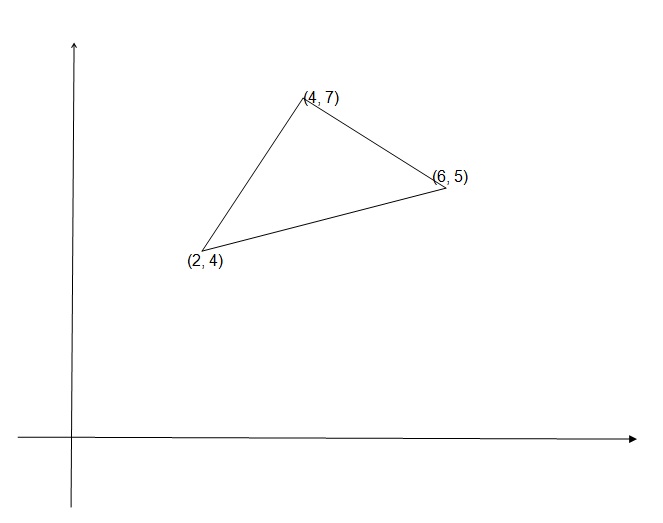 Pyramid base
Pyramid base
Then the volume is

