Question

The base of a triangular pyramid is a triangle with corners at `(6 ,7 )`, `(3 ,1 )`, and `(5 ,9 )`. If the pyramid has a height of `8`, what is the pyramid's volume?

Answer 1

`color(green)(V = 16.5781)` cubic units

Explanation:

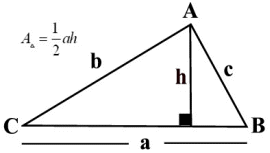
Triangle Area `A = (1/2) * a * h`

`BC = a = sqrt((5-3)^2 + (9-1)^2) = 8.2462`

Slope of BC `m_a = (9-1) / (5-3) = 4`

Equation of BC

`(y - 1) / (9 - 1) = (x - 3) / (5 - 3)`

`2y - 2 = 8x - 24`

`y - 4x = -11` Eqn (1)

Slope of altitude through A is `m__h = -1/4`

Equation of altitude h is

`y - 7 = -(1/4) (x - 6)`

`4y + x = 34` Eqn 2

Solving equations (1) & (2), we get the coordinates of D, the base of altitude h

#D (78/11, 128/17)

Height of altitude `AD = h = sqrt((6-(78/17))^2 + (7 - (128/17))^2) = 1.5078`

Area of Triangle `color(green)A = (1/2) b h = (1/2) * 8.2462 * 1.5078 = color(green)(6.2168)`

Volume of Pyramid V = (1/3) * Base Area * Height

`color(green)(V = (1/3) 6.2168 * 8 = 16.5781)`