The base of a triangular pyramid is a triangle with corners at #(7 ,6 )#, #(4 ,3 )#, and #(1 ,8 )#. If the pyramid has a height of #6 #, what is the pyramid's volume?
1 Answer
The volume of the pyramid is 24.
Explanation:
Let
When we need to calculate area of an arbitrary triangle with integer coordinates of vertices, it could be useful to draw it and then a rectangle around it. The rectangle should have sides parallel to axes.
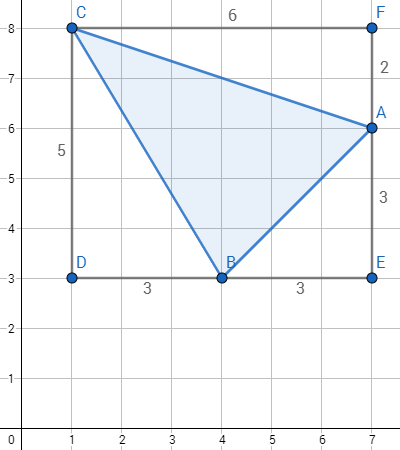
Now we can calculate area of the rectangle and subtract areas of white right triangles. It's much easier than calculating blue triangle's area directly.
So
Now we have base area

