Question

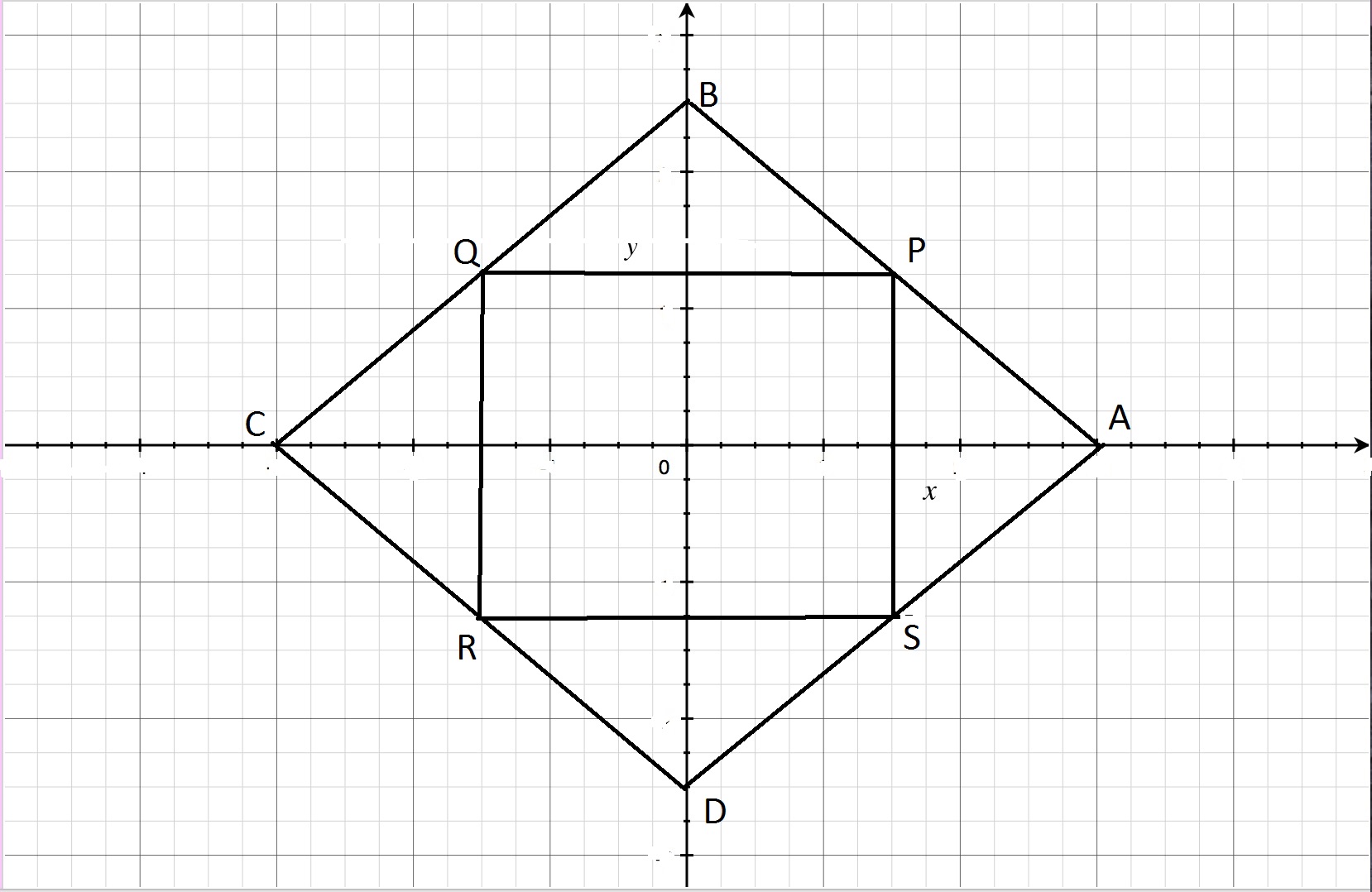
The coordinates for a rhombus are given as (2a, 0) (0, 2b), (-2a, 0), and (0.-2b). How do you write a plan to prove that the midpoints of the sides of a rhombus determine a rectangle using coordinate geometry?

Answer 1

Please see below.

Explanation:

Let the points of rhombus be `A(2a, 0), B(0, 2b), C(-2a, 0)` and `D(0.-2b)`.

Let midpoints of `AB` be `P` and its coordinates are `((2a+0)/2,(0+2b)/2)` i.e. `(a,b)`. Similarly midpoint of `BC` is `Q(-a,b)`; midpoint of `CD` is `R(-a,-b)` and midpoint of `DA` is `S(a,-b)`.

It is apparent that while `P` lies in Q1 (first quadrant), `Q` lies in Q2, `R` lies in Q3 and `S` lies in Q4.

Further, `P` and `Q` are reflection of each other in `y`-axis, `Q` and `R` are reflection of each other in `x`-axis, `R` and `S` are reflection of each other in `y`-axis and `S` and `P` are reflection of each other in `x`-axis.

Hence `PQRS` or midpoints of the sides of a rhombus `ABCD` form a rectangle.