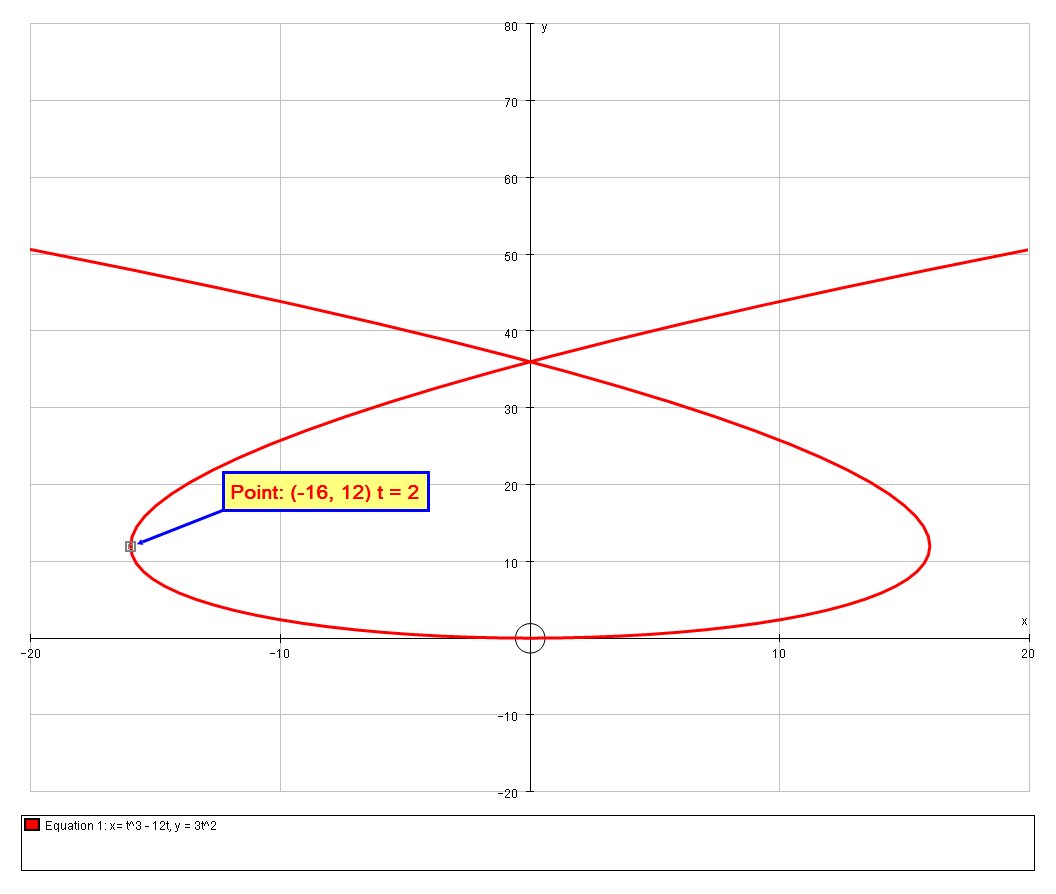
The curve has a parametric equation of #x=(t^3)-12t# and #y=3(t^2)#, how would you find the two points the parameter t=2 crosses the curve?
1 Answer
Oct 7, 2017
We have parametric equations:
# x= t^3 - 12t #
# y = 3t^2 #
When
# x= 8 - 24 = -16#
# y = 3*4 \ \ \ \ = 12 #
So, there is only one point associated with
The graph of the curve is as follows: