Question

The diagonal of a square has length `12sqrt2` ft. How do you find the length of the side of the square?

Answer 1

length of side: `12` feet

Explanation:

Since the figure is a square, it's sides have the same length; Lets call this length `s`

The diagonal forms a hypotenuse, `h`, with two of the sides
and, based on the Pythagorean Theorem,
`color(white)("XXX")s^2+s^2=h^2`
and since the diagonal (`h`) is given as having a length of `12sqrt(2)`,
we have
`color(white)("XXX")2s^2=(12sqrt(2))^2=12^2 * (sqrt(2))^2= 12^2 * 2`

`color(white)("XXX")rarr s^2=12^2`

and since (in the normal world) lengths can not be negative:
`color(white)("XXX")s=12`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

An easier way to see this is to remember the standard right triangle (often used in trigonometry):

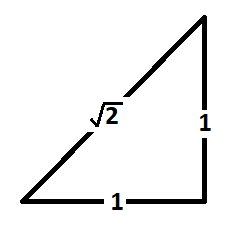
and realize the given triangle is a similar triangle simply scaled up by a factor of `12`