The following reaction was monitored as a function of time: #AB -> A + B#. A plot of #1/[AB]# versus time yields a straight line with slope #5.6xx10^(-2) (M.s)^-1#. What is the value of the rate constant (k) for this reaction temperature?

Question

19473 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-09T22:06:50

#sf(k=5.6xx10^(-2)color(white)(x)"mol"^(-1)."l"."s"^(-1))#

This looks like a 2nd order reaction:

#sf(ABrarrA+B)#

For which the rate of disappearance of #sf(AB)# can be written:

#sf((d[AB])/(dt)=-k[AB]^2)#

Integrating this gives:

#sf((1)/([AB])=(1)/([AB]_0)+kt)#

Where #sf([AB]_0]# is the initial concentration and #sf(k)# is the rate constant.

This means a plot of #sf((1)/([AB])# against #sf(t)# will give a gradient of #sf(k)# and an intercept of #sf((1)/([AB]_0))#:

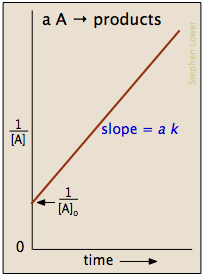
chemwiki.ucdavis.edu

The graph is a straight line of the form #sf(y=mx+c)# so the rate constant is equal to the gradient of the line:

#:.##sf(k=5.6xx10^(-2)color(white)(x)"mol"^(-1)."l"."s"^(-1))#