The half-life of P-32 is 14.30 days. How many milligrams of a 20.00 mg sample of P-32 will remain after 85.80 days?

Question

18503 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-08-04T20:27:27

The amount remaining is #=0.3125mg#

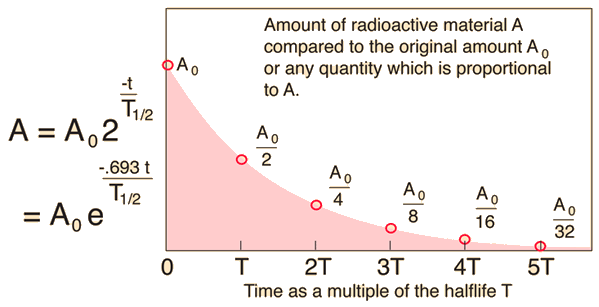
enter image source here

The half life is #t_(1/2)=14.3d#

This means that after #14.3# days #50%# of the sample will remain

The time is #T=85.8#days

This is equal to #=85.8/14.3=6# half lives

Therefore,

The amount remaining is #=1/2^6*20=0.3125mg#

We can solve this problem with the equation

#m=m_0e^(-lambdat)#

The radioactive constant is #lambda=ln2/t_(1/2)=ln2/14.3#

Therefore,

#m=20*e^(-ln2*85.3/14.3)=20*e^(-6ln2)=20*e^-ln(2^6)=20*e^-ln64#

#m=20/64=0.3125mg#