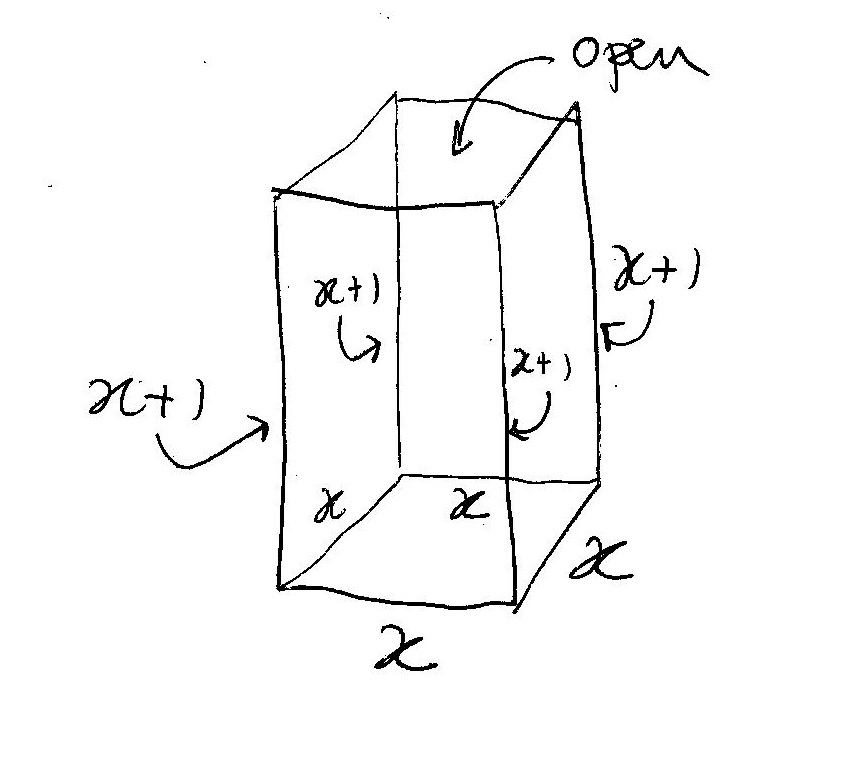
The height of an open box is 1 cm more than the length of a side of its square base. if the open box has a surface area of 96 cm (squared), how do you find the dimensions.?
2 Answers
The dimensions of the box would be length= width = 4cms and height = 5 cms
Explanation:
Let the side of the square base be x cms, then height would be x+1 cms.
Surface area of the open box, would be area of the base and area of its four faces, =xx +4x*(x+1)
Therefore
The dimensions of the box would be length= width = 4cms and height = 5 cms
You'll find
Explanation:
Call the length of the side of the square base
so:
Surface area
Using the Quadratic Formula:
The useful solution will then be:

