The length of a rectangle is 4 times its width x. If the rectangle is inscribed in a circle, how do you determine the area of the circle as a function of x?
3 Answers
Explanation:
Firstly, find the length of half a diagonal across the rectangle.
The length of a diagonal can be found using pythagorus:
Then you half this length
This is the radius of the circle. Therefore as the area of a circle is
See explanation.
Explanation:
If a rectangle is inscribed in a circle, then its diameter is the diagonal of the rectangle.
If we use the given information and the Pythagorean theorem we get:
#l^2+w^2=d^2#
#(4x)^2+x^2=d^2#
#d^2=17x^2#
#d=xsqrt(17)#
The circle radius is half of its diameter, so:
#r=(xsqrt(17))/2#
To calculate the area we use:
The area is then:
#A=17/4pix^2#
Explanation:
The width of the rectangle is
Width
Length
When a quadrilateral is inscribed in a circle, the centre of the quadrilateral falls exactly on the centre of the circle.
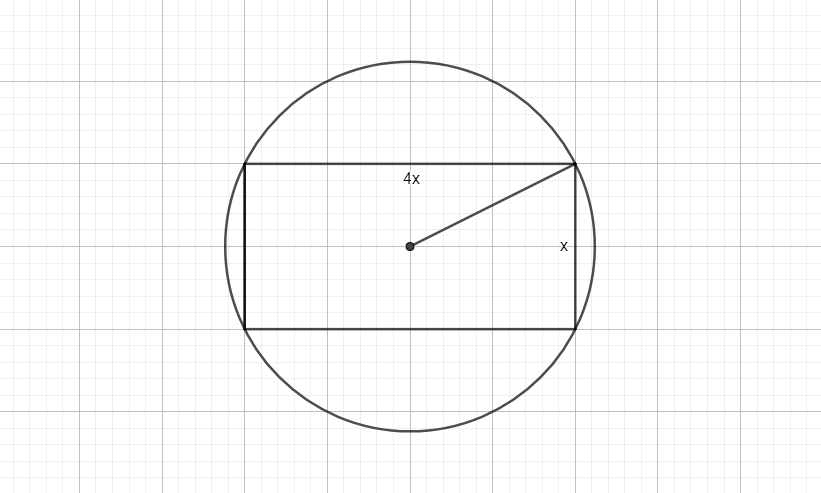
As you can see, the radius of the circle is equivalent to half the length of the diagonal of the rectangle.
Now that we have the radius, let's find the area of the circle using the formula of the area of a circle:
The area of the circle is


