Question

The length of a rectangle is four times its width. If the area of the rectangle is 256m^2 how do you find its perimeter?

Answer 1

The perimeter of the rectangle is `80` meters.

Explanation:

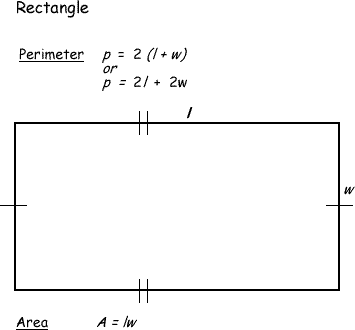
Here are two formulas for rectangles that we will need to solve this problem, where `l` = length and `w` = width:

(pinterest.com)

In this question, we know that:
`l = 4w`
`A = 256 m^2`

First, let's find the width:
`lw = 256`

Let's substitute the value of `4w` for `l`:
`(4w)w=256`

Multiply the `w`:
`4w^2 = 256`

Divide both sides by `4`:
`w^2 = 64`

`w = 8`

So we know that the width is `8`.

Since `l = 4w` and we have `w`, we can find the value of `l`:
`4(8)`
`32`

The width is `8` meters and the length is `32` meters.

`-------------------`

Now we find the perimeter. Remember the formula for the perimeter is `2l + 2w` as stated earlier. Since we have the values of `l` and `w`, we can solve this:
`2(32) + 2(8)`
`64 + 16`
`80`

The perimeter of the rectangle is `80` meters.

Hope this helps!