The perimeter of a garden is 62 yd and the area is 120yd^2, how do you find the dimensions?
1 Answer
Sep 23, 2015
I found
Explanation:
I supposed that you had a rectangular garden:
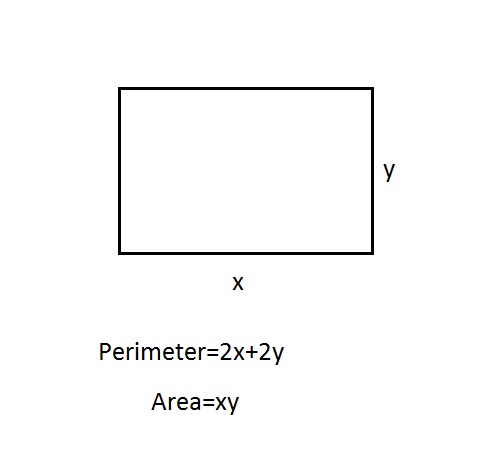
So:
From the second:
Using the Quadratic Formula:
You get two solutions:
We can choose the first,

