Question

The resistances in the following figure are in ohm. Then the effective resistance between the points A and B is? (A) 2`Omega` (B) 3 `Omega` (C) 6`Omega` (D) 36 `Omega`

Answer 1

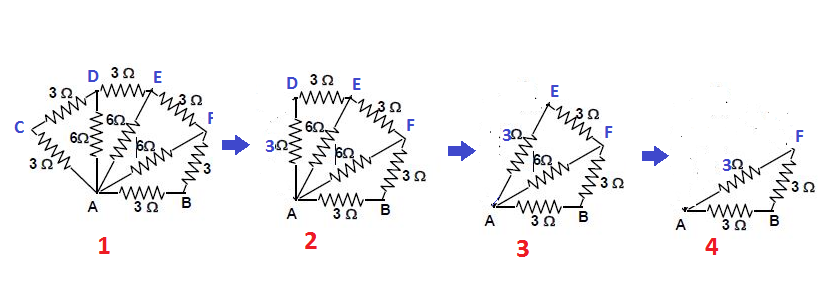
In the given network for resistor if we consider the portion ACD , we observe that across AD resistor `R_(AC)` and `R_(CD)`are in series and `R_(AD)` is parallel . So the equivalent resistance of this portion across AD becomes

`R_"eqAD"=1/(1/(R_(AC)+R_(CD))+1/R_(AD))=1/(1/((3+3))+1/6)=3Omega`

and we get equivalent network `color(red)2`

similarly if we proceed , we finally reach at figure `color(red)4` i.e.equivalent network `ABF` and the equivalent resistance of the given network across AB becomes

`R_"eqAB"==1/(1/(R_(AF)+R_(FB))+1/R_(AB))=1/(1/((3+3))+1/3)=2Omega`