Question

The terminal side of θ lies on a given line in the specified quadrant. Find the values of the six trigonometric functions of θ by finding a point on the line? Line y = 1/6x Quad: III

Answer 1

You have to start by finding a point that lies on this line. I think the simplest would be `(-6, -1)` (since we are in quadrant III, both the x and y axis have to have negative values).

We now draw an imaginary triangle, as shown in the following diagram.

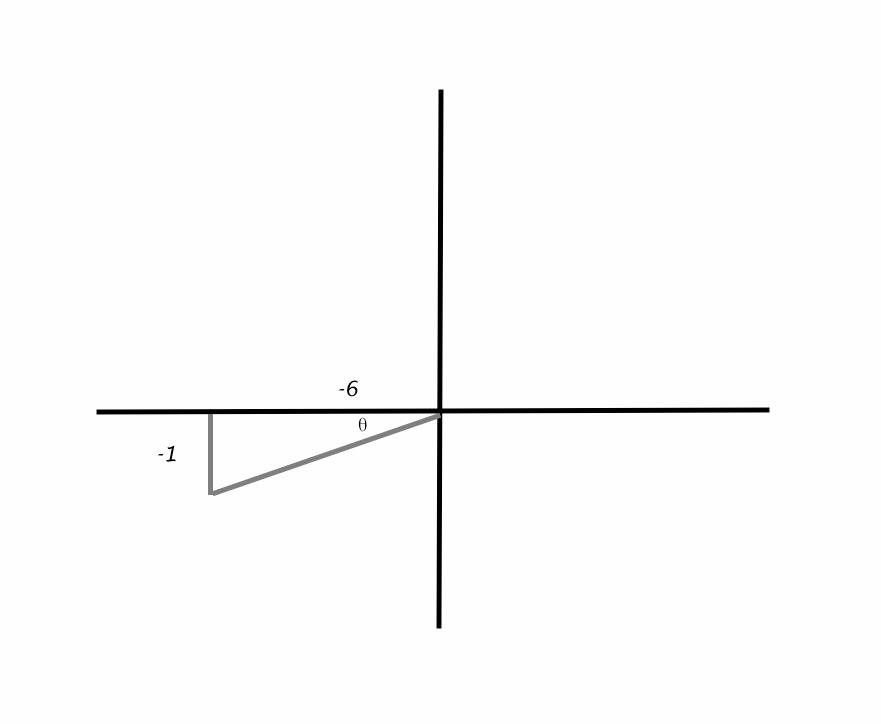
We can now clearly see that our side opposite `theta` measures `1` unit and our side adjacent `theta` measures `6` units.

We must finally find the hypotenuse prior to determining the ratios. By pythagorean theorem:

`a^2 + b^2 = c^2`

`(-1)^2 + (-6)^2= c^2`

`1 + 36 = c^2`

`c^2 = 37`

`c = +-sqrt(37)`

However, the hypotenuse can never have a negative length, so we can only accept the positive solution. We can now find our ratios.

`sintheta = "opposite"/"hypotenuse" = -1/sqrt(37) = -sqrt(37)/37`

`csctheta = 1/sintheta = 1/("opposite"/"hypotenuse") = "hypotenuse"/"opposite" = sqrt(37)/(-1) = -sqrt(37)`

`costheta = "adjacent"/"hypotenuse" = -6/sqrt(37) = (-6sqrt(37))/37`

`sectheta = 1/costheta = 1/("adjacent"/"hypotenuse") = "hypotenuse"/"adjacent" = sqrt(37)/(-6) = -sqrt(37)/6`

`tantheta = "opposite"/"adjacent" = -1/(-6) = 1/6`

`cottheta = 1/tantheta = 1/("opposite"/"adjacent") = "adjacent"/"opposite" = -6/(-1) = 6`

Hopefully this helps!