The volume of a rectangular prism is #3x^3+34x^2+72x-64#, if the height is x+4, what is the area of the base of the prism?

Question

4808 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-07T14:28:05

#3x^2 +22x - 16# square units.

The formula for volume of a prism is #V = A_"base" * h#. Therefore,

#3x^3 + 34x^2 + 72x - 64 = (x + 4)A_"base"#

#A_"base" = (3x^3 + 34x^2 + 72x - 64)/(x+ 4)#

Use either synthetic or long division. I will use long division but either methods work.

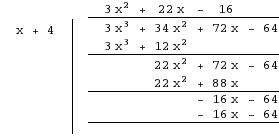
enter image source here

Therefore, the quotient is #3x^2 + 22x - 16#. This means the area of the base is #3x^2 + 22x - 16# square units.

Hopefully this helps!