Three slabs are stacked vertically with the lowest slab being on wheels as shown below. An applied force of #44N# acts horizontally on the bottom slab. How do you find the answers to the following questions?
a. What is the acceleration of the system if the slabs do not slip?
b. How much friction acts between the bottom and middle slab?
c. What coefficient of friction is necessary to prevent slipping between the middle and bottom slab?
d. How much friction is needed between the top and middle slab to prevent slipping?
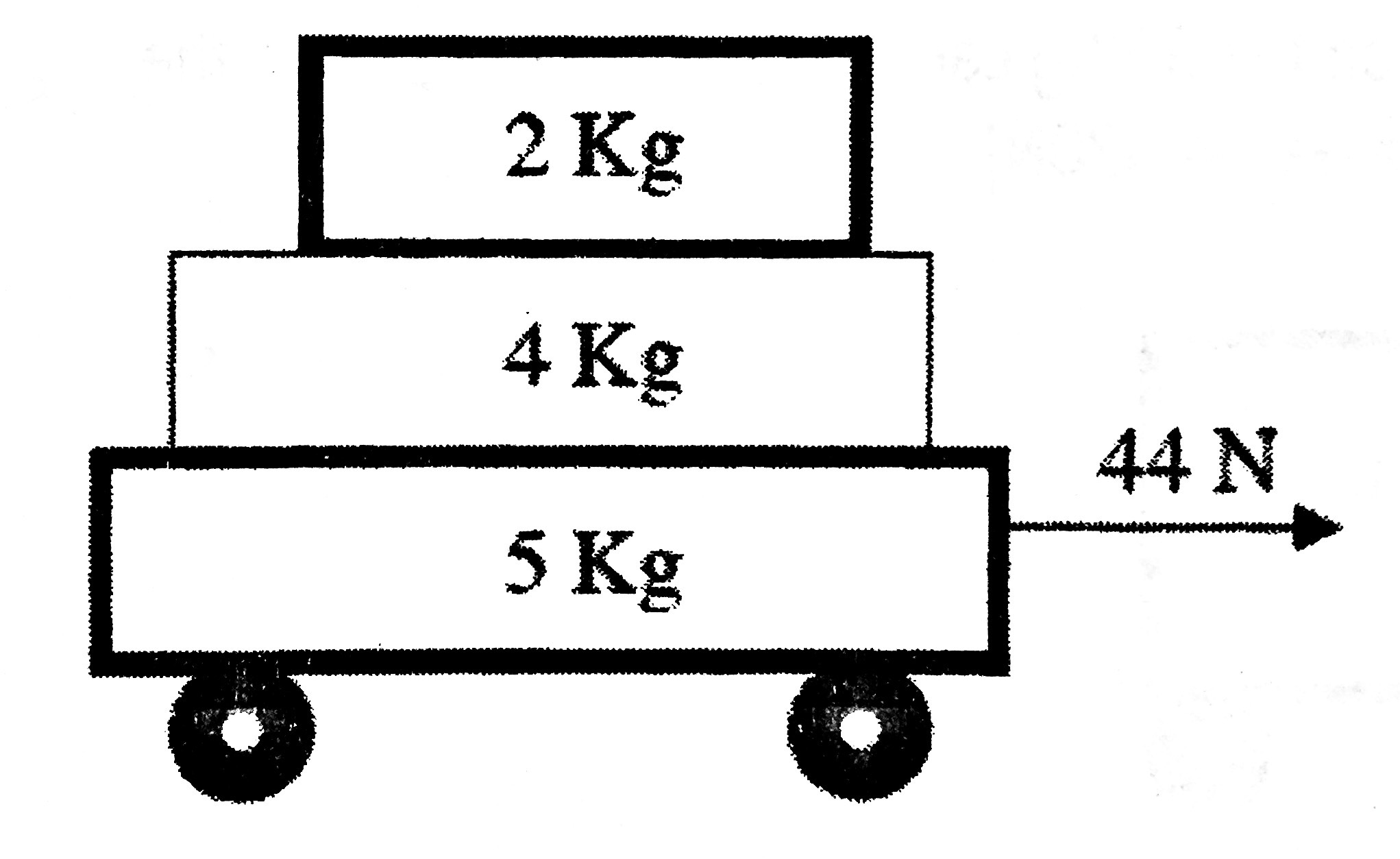
a. What is the acceleration of the system if the slabs do not slip?
b. How much friction acts between the bottom and middle slab?
c. What coefficient of friction is necessary to prevent slipping between the middle and bottom slab?
d. How much friction is needed between the top and middle slab to prevent slipping?
1 Answer
a. The slabs do not slip, three blocks act as one.
Mass of system of blocks
Force applied
Using Newtons Second Law of motion
#vecF=mveca#
Inserting given values
#44=11|veca|#
#=>|veca|=44/11=4ms^-2# ,
direction being the direction of applied force.
b. Mass of top two blocks resting on the lowest block
Acceleration of top two blocks
Force applied on top two blocks
As the blocks do not slip, this must be equal to Force of friction between middle and lowest block.
c. We know that
Normal Reaction
#=mumg#
From Newton's Third Law of motion we know that Action and reaction are equal and opposite.
Taking
d. Action Force applied by top block on the middle block
As explained in b.
To prevent blocks from slipping friction required between top and middle blocks
