Question

Two rhombuses have sides with lengths of `1`. If one rhombus has a corner with an angle of `pi/12` and the other has a corner with an angle of `pi/3`, what is the difference between the areas of the rhombuses?

Answer 1

Difference in areas between the two rhombuses is

`A_d = 0.6072` sq units

Explanation:

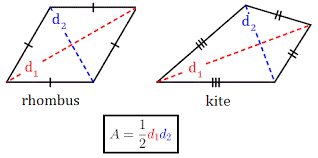
Area of a rhombus `A_r = (1/2) d_1 d_2`

Area of a parallelogram `A_p = b h = b a sin theta`

Rhombus is a special type of a parallelogram with all 4 sides equal.

`A_r = a * a * sin theta = a^2 sin theta`

Given `a = 1, theta = pi / 12`

`A_1 = 1^2 sin (pi/12) = 0.2588`

Area of second rhombus

`A_2 = 1^2 sin (pi/3) = sqrt 3 / 2 = 0.866`

Difference in areas between the two rhombuses is

`A_d = 0.866 - 0.2588 = 0.6072`