Question

Two rhombuses have sides with lengths of `4`. If one rhombus has a corner with an angle of `(7pi)/12` and the other has a corner with an angle of `(3pi)/4`, what is the difference between the areas of the rhombuses?

Answer 1

Area difference: `4.1411` (approx.)

Explanation:

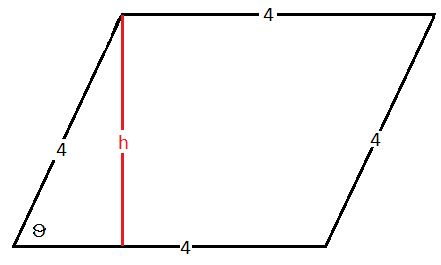
Te Area of a rhombus is `s xx h`
where `s` is the length of a side and `h` is it's height.

The height of a rhombus is given by the formula
`color(white)("XXX")h=s xx sin(theta)`
where `theta` is an interior angle of the rhombus.

For rhombus `R1` with `theta=(7pi)/12` and `s=4`
`color(white)("XXX")"Area"_(R1) = 4 xx 4 xx sin((7pi)/12) ~~15.54481`

For rhombus `R2` with `theta=(3pi)/4` and `s=4`
`color(white)("XXX")"Area"_(R2)=4 xx 4 xx sin((3pi)/4) ~~11.31371`

The difference in the ares of the rhombi is
`color(white)("XXX")15.54481 - 11.31371 = 4.1411`

Answer 2

`4.14`

Explanation:

(Using trigonometry)

We need to calculate the area of these rhombus' with given sides and an angle.And,we need to subtract their areas.

Here comes a handy formula

`color(blue)("Area of rhombus"=s^2sin(a)`

Where,

`color(orange)(s="side"and a="one of the angles"`

So,we calculate the area of the first rhombus

`rarrs^2sin(a)`

`rarr4^2sin((7pi)/12)`

`rarr16sin(105^circ)`

`rarr16*0.96`

`color(green)(rArr15.45`

Now we calculate the area of the second rhombus

`rarrs^2sin(a)`

`rarr4^2sin((3pi)/4)`

`rarr16sin(135^circ)`

`rarr16*0.7`

`color(green)(rArr11.31`

Subtract the areas

`rArr15.45-11.31=4.14`

`:."The difference between the area are approximately"` `color(blue)(4.14`

`("Note: these are approximations only")`