Question

Using the limit definition, how do you find the derivative of `f(x) = 3x - x^2`?

Answer 1

When finding the derivative using first principles, we use
`ƒ'(x) = lim_(h -> 0) ((ƒ(x + h) - ƒ(x))/h)`

Explanation:

Since we can't evaluate immediately (a denominator equal to zero in mathematics is undefined), we will have to simplify somewhat. Also, note that the proper formatting for the formula is shown in the following image--I am just unsure how to write it on Socratic. I'm sorry for any inconvenience this may cause.

`f'(x) = lim_(h -> 0) ((3(x + h) - (x + h)^2 - (3x - x^2))/h)`

`f'(x) = lim_(h -> 0) ((3x + 3h - (x^2 + 2xh + h^2) - 3x + x^2))/h`

`f'(x) = lim_(h-> 0) ((3x + 3h - x^2 - 2xh - h^2 - 3x + x^2))/h`

`f'(x) = lim_(h->0) ((3h - 2xh - h^2))/h`

`f'(x) = lim_(h->0) (cancel(h)(3 - 2x - h))/cancel(h)`

`f'(x) = lim_(h->0) (3 - 2x - h)`

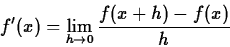
Now we can evaluate:

`f'(x) = 3 - 2x`

Therefore, the derivative of `f(x) = 3x - x^2` is `f'(x) = 3 - 2x`, or in alternative notation `dy/dx = 3 - 2x`

Hopefully this helps!