Question

Using the pythagorean theorem, how do you solve for the missing side given a = 14 and b = 13?

Answer 1

`c=sqrt(a^2 + b^2) = sqrt(14^2 + 13^2) =sqrt(365) ~= 19.1`

Explanation:

The Pythagorean Theorem applies to right angle triangles, where the sides `a` and `b` are those which intersect at right angle. The third side, the hypotenuse, is then `c`

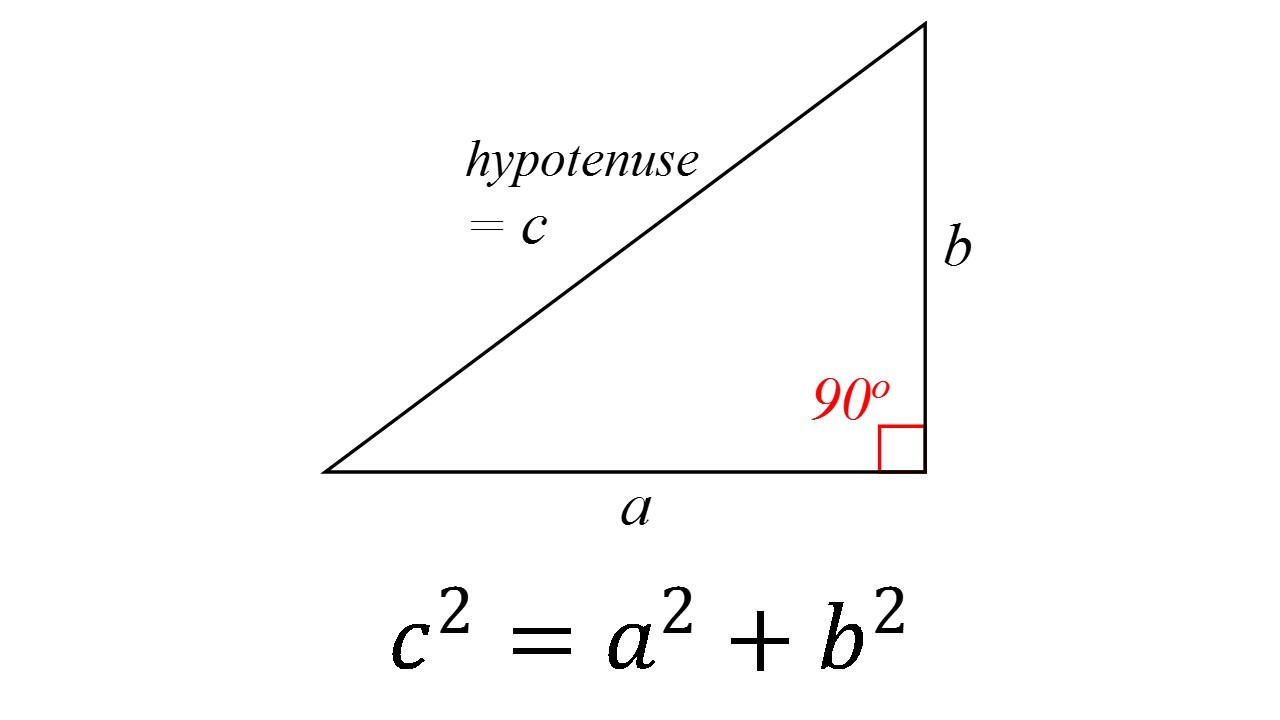
In our example we know that `a=14` and `b=13` so we can use the equation to solve for the unknown side `c`:

`c^2 = a^2 + b^2`

or

`c=sqrt(a^2 + b^2) = sqrt(14^2 + 13^2) =sqrt(365) ~= 19.1`