First, isolate the sine
#sin(2x)=1#
Now, take a look at your unit circle
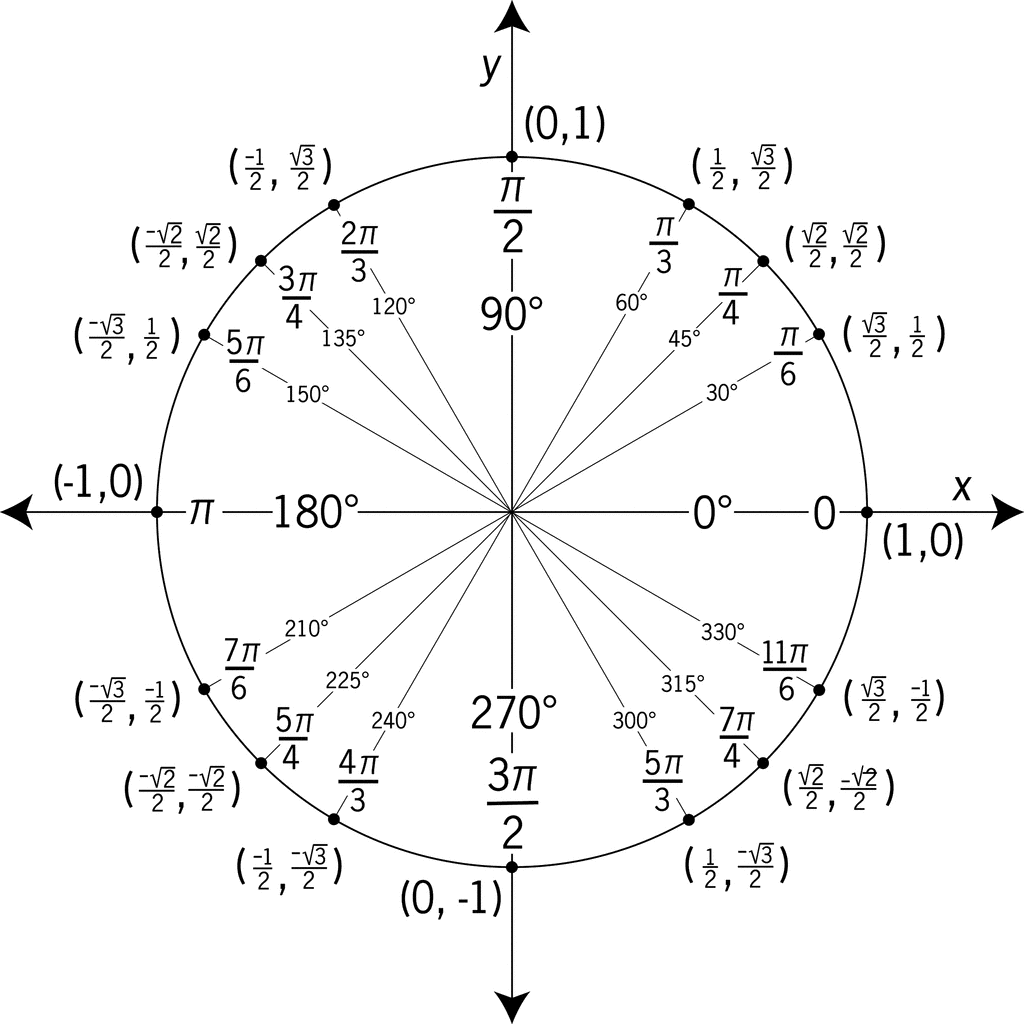
Now, the sine correspond to the #y# axis, so we can see that the only point between #0# and #2pi# where the sine is #1# is #pi/2# radians, so we have:
#2x = pi/2#
We want to solve for x, so
#x = pi/4#
However, remember that the period of the normal sine wave is #2pi#, but since we're working with #sin(2x)#, the period has changed; basically what we know is that there is a constant #k# that will act as the period, so:
#2(pi/4 + k) = pi/2 + 2pi#
#pi/2 + 2k = pi/2 + 2pi#
#2k = 2pi#
#k = pi#
And since #pi/4 + pi# or #5pi/4# is between #0# and #2pi#, that enters our set of solutions.
#S={pi/4,5pi/4}#




