Question

What are the coupling constants (`J`)?

Answer 1

The coupling constant `J` is pretty much the peak-to-peak distance, usually reported in `"Hz"`. Matching it up with other nearly-identical coupling constants elsewhere in the spectrum usually tells you which protons are near which others.

---

For example:

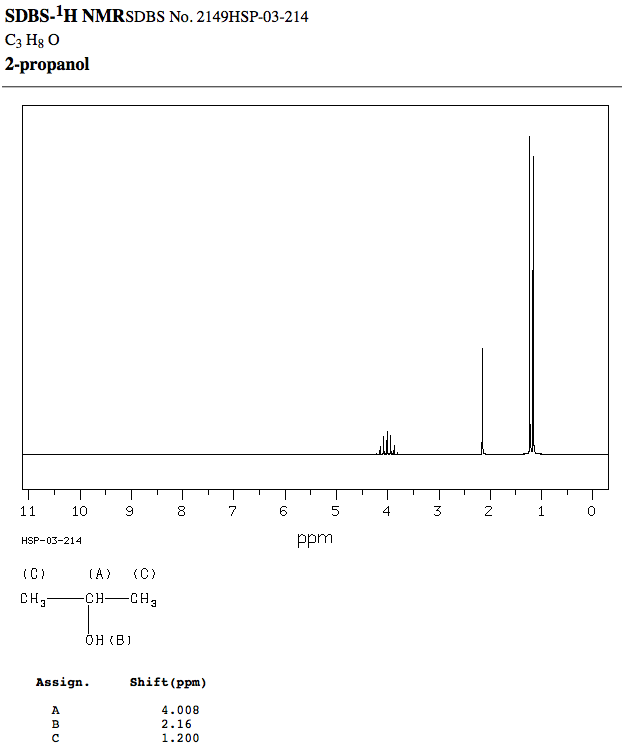
Peak Data:
`"Hz"" "" " "" " ppm"" ""Intensity"`

Proton A:
`"371.56"" ""4.149"" ""24"`
`"365.38"" ""4.080"" ""56"`
`"359.25"" ""4.012"" ""72"`
`"353.13"" ""3.943"" ""60"`
`"347.06"" ""3.876"" ""28"`

Proton B:
`"193.00"" ""2.155"" ""335"`

Proton C:
`"110.44"" ""1.234"" ""1000"`
`"108.19"" ""1.209"" ""27"`
`"104.31"" ""1.165"" ""939"`
`"102.06"" ""1.140"" ""25"`

What is shown here for proton A is that `"4.008 ppm"` is the average chemical shift of the 1-4-6-4-1 pattern (according to Pascal's triangle) from the rightmost peak to the leftmost peak, and the entire signal there has multiple peaks. The peaks split like so:

1 `->` 1-1 `->` 1-2-1 `->` 1-3-3-1 `->` 1-4-6-4-1

It is not visible in this zoom, but the distance between each peak is roughly identical. This distance is the numerical equivalent of the coupling constant `J` in `"Hz"`. For proton A:

`4.149 - 4.080 = "0.069 ppm"`
`4.080 - 4.012 = "0.068 ppm"`
`4.012 - 3.943 = "0.069 ppm"`
`3.943 - 3.876 = "0.067 ppm"`

Interestingly enough, if you look at protons C at the averaged `"1.200 ppm"`, you would also see that that doublet has the same `J` value (ideally that doublet should have both peaks at identical intensities too, but the shimming was not perfect, so they are a bit off). For proton C:

`1.234 - 1.165 = "0.068 ppm"`

From the identical (or nearly-identical) coupling constant, you can determine which protons are "communicating" with each other and thus which protons they neighbor.

If you take this number and multiply it by the `"MHz"` of your NMR, you get the coupling constant in `"Hz"`. So, if your NMR's magnetic field frequency is `"89.56 MHz"` (like for this particular spectrum), then:

`"0.068 ppm" * "89.56 MHz"`

`= 0.068 ("Hz")/("MHz") * "89.56 MHz"`

`= color(blue)"6.09 Hz"`

Indeed, for proton C, `110.44 - 104.31 = "6.13 Hz" ~~ "6.09 Hz"`.

Therefore, without seeing the structure of the analyzed molecule, you can still figure out that proton A and protons C are coupling/"communicating" with each other.